
分析 (1)根据题意和配方法可以解答本题;
(2)根据题意和(1)中的解答可以解答本题.
解答 解:(1)最小值是0,
理由:${a^2}-2\sqrt{3}a+3={a^2}-2\sqrt{3}a+{(\sqrt{3})^2}={(a-\sqrt{3})^2}$,
∵${(a-\sqrt{3})^2}≥0$,
∴${a^2}-2\sqrt{3}a+3$的最小值是0;
(2)最小值是0,
理由:$\frac{a+b}{2}$-$\sqrt{ab}$=$\frac{(\sqrt{a}-\sqrt{b})^{2}+2\sqrt{ab}}{2}-\sqrt{ab}$,
∵$(\sqrt{a}-\sqrt{b})^{2}$≥0,
∴$\frac{(\sqrt{a}-\sqrt{b})^{2}+2\sqrt{ab}}{2}-\sqrt{ab}$≥$\frac{0+2\sqrt{ab}}{2}-\sqrt{ab}$=0,
即$\frac{a+b}{2}$-$\sqrt{ab}$有最小值,最小值是0.
点评 本题考查配方法、非负数的性质,解答本题的关键是明确题意,利用配方法和非负数的性质解答.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
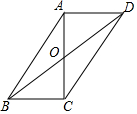 如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.
如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
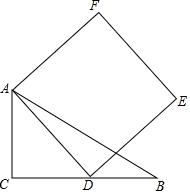 如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.
如图.己知△ABC中.∠C=90°,AC=3,BC=4.动点D在边BC上.以AD为边作正方形ADEF.在点D从点C移动至点B的过程中.点E移动的路线长为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
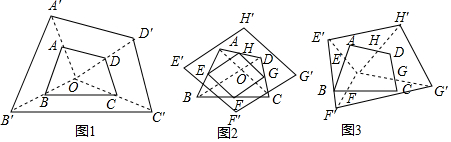
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{84}{83}$和$\frac{88}{87}$ | B. | $\frac{86}{85}$和$\frac{88}{87}$ | C. | $\frac{85}{84}$和$\frac{87}{86}$ | D. | $\frac{86}{85}$和$\frac{87}{86}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 0 | C. | 0或3 | D. | 非上述答案 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com