
 计算:
计算:分析 (1)根据线段的和差,可得(MB+CN)的长,根据线段中点的性质,可得(AB+CD)的长,根据线段的和差,可得答案;
(2)设这个角为x,则补角为(180°-x),余角为(90°-x),再由补角比它的余角的3倍多17°,可得方程,解出即可.
解答 解:(1)由线段的和差,得
MB+CN=MN-BC=11-3=8,
由M是线段AB的中点,N是线段CD的中点,得
AB+CD=2MB+2CN=2(MB+CN)=16,
由线段的和差,得
AD=AB+BC+CD=16+3=19.
(2)设这个角为x,则补角为(180°-x),余角为(90°-x),
由题意得,180°-x=3(90°-x)+17°,
解得:x=53.5.
故这个角的度数是53.5°.
点评 本题考查了两点间的距离,利用了线段的和差,线段中点的性质.同时考查了余角和补角的知识,解答本题的关键是掌握互余的两角之和为90°,互补的两角之和为180°.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
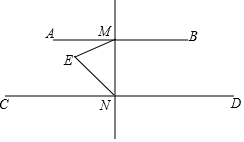 如图,AB∥CD,MN⊥AB于M.
如图,AB∥CD,MN⊥AB于M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com