练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．设x1，x2是方程x2-2x-1=0的两个实数根，则$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$的值是（　　）
    A．-6B．-5C．-6或-5D．6或5

    分析 先根据根与系数的关系得到x1+x2=2，x1x2=-1，然后利用整体代入的方法计算．

    解答 解：根据题意得x1+x2=2，x1x2=-1，
    所以$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{（{x}_{1}+{x}_{2}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=-6．
    故选A．

    点评 本题考查了根与系数的关系，解题的关键是能够将代数式进行正确的变形，难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    14．估计$\sqrt{5}$+1的值在（　　）
    A．1和2之间B．2和3之间C．3和4之间D．4和5之间

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，从一块直径为4$\sqrt{2}$cm的圆形纸片上剪出一个圆心角为90°的扇形ABC，使点A，B，C在圆周上，将剪下的扇形作为一个圆锥的侧面，则这个圆锥的底面圆的半径是（　　）
    A．2$\sqrt{2}$cmB．$\sqrt{2}$cmC．1 cmD．2cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列计算正确的是（　　）
    A．a+a=a2B．a•a2=a3C．（-a3）2=a9D．（3a）3=9a3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

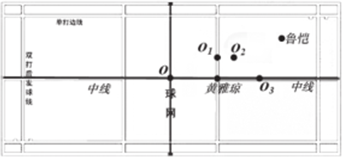    19．2017 全英羽毛球公开赛混双决赛，中国组合鲁恺/黄雅琼，对阵马来西亚里约奥运亚军陈炳顺/吴柳萤，鲁恺/黄雅琼两名小将的完美配合结果获胜．如图是羽毛球场地示意图，x 轴平行场地的中线，y 轴平行场地的球网线，设定鲁恺的坐标是（3，1），黄雅琼的坐标是（0，-1），则坐标原点为（　　）
    A．OB．O1C．O2D．O3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

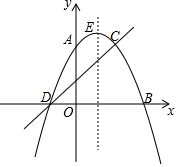    9．如图，抛物线y=ax2+bx+c过A（0，4），B（4，0），C（2，4）三点，与x轴另一交点记作D，直线y=kx+n过C、D两点．
    （1）求抛物线与直线CD的解析式；
    （2）在抛物线y=ax2+bx+c的对称轴上是否存在一点P，使得PA+PD最小，若存在，请写出点P的坐标，并求出PA+PD的最小值；若不存在，请说明理由；
    （3）若点E为抛物线y=ax2+bx+c的顶点，连接EC、ED，则在直线y=kx+n的上方的抛物线上是否存在一点M，使得S△MCD=S△DEC，若存在，直接写出M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．事件A：掷一次骰子，向上一面的点数是5；事件B：买一张彩票，有一注号码中奖了，则（　　）
    A．事件A和B都是随机事件
    B．事件A是随机事件，事件B是不可能事件
    C．事件A是必然事件，事件B是随机事件
    D．事件A和事件B都是必然事件

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知x＞0，且x2-16=0，求$\sqrt{3x+5}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知x，y是有理数，且（1+$\sqrt{3}$）x+（1-$\sqrt{3}$）y-12=0，求x，y的值．

    查看答案和解析>>

    同步练习册答案