
| A. | 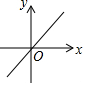 | B. | 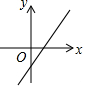 | C. | 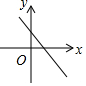 | D. | 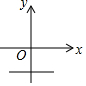 |
科目:初中数学 来源: 题型:选择题
| A. | -($\frac{3}{4}$x+1)=5 | B. | -$\frac{3}{4}$x+1=5 | C. | $\frac{3}{4}$x-1=5 | D. | -x($\frac{3}{4}$x+1)=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
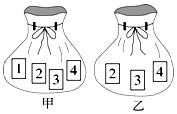 如图,甲袋内共有4张牌,牌面分别标记数字1,2,3,4;乙袋内共有3张牌,牌面分别标记数字2,3,4.甲袋中每张牌被取出的机会相等,且乙袋中每张牌被取出的机会也相等.分别从甲乙两袋中各随机抽取一张牌,请用列表或画树形图的方法,求抽出的两张牌面上的数字之和大于6的概率.
如图,甲袋内共有4张牌,牌面分别标记数字1,2,3,4;乙袋内共有3张牌,牌面分别标记数字2,3,4.甲袋中每张牌被取出的机会相等,且乙袋中每张牌被取出的机会也相等.分别从甲乙两袋中各随机抽取一张牌,请用列表或画树形图的方法,求抽出的两张牌面上的数字之和大于6的概率.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
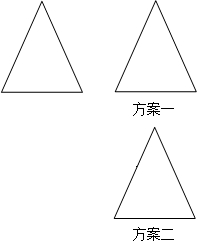 张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.
张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com