
【题目】如图,△ABC是等边三角形,D是BC的中点. 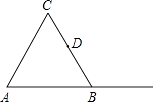
(1)作图: ①过B作AC的平行线BH;
②过D作BH的垂线,分别交AC,BH,AB的延长线于E,F,G.
(2)在图中找出一对全等的三角形,并证明你的结论.
科目:初中数学 来源: 题型:
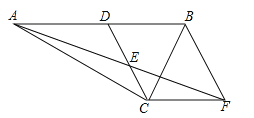
【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习成为现代人的时尚,某市有关部门统计了最近6个月到图书馆的读者的职业分布情况,并做了下列两个不完整的统计图. 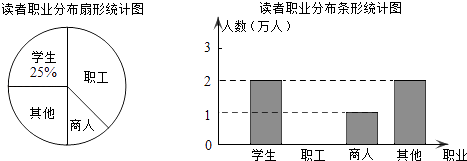
(1)在统计的这段时间内,共有万人次到图书馆阅读,其中商人占百分比为%;
(2)将条形统计图补充完整;
(3)若5月份到图书馆的读者共28000人次,估计其中约有多少人次读者是职工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数图象的顶点在原点O,经过点A(1, ![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.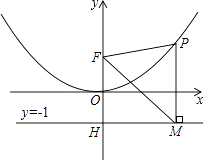
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
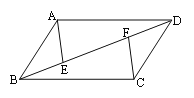
【题目】如图,四边形ABCD中,AB=CD,AB∥CD,点E、F在线段BD上,且BE=DF,连接AE、CF.
(1)指出线段AE与CF的关系,并说明理由;
(2)若将题中的条件“点E、F在线段BD上”改为“点E、F在直线BD上” ,那么(1)中的结论还一定能成立吗?若能,直接写出结论;若不能,请举出反例加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断正误,并说明理由(1)给定一组数据,那么这组数据的众数有可能不唯一________;理由________(2)给定一组数据,那么这组数据的平均数一定是这组数据中的一个数________;
理由________(3)n个数的中位数一定是这n个数中的某一个________;理由________(4)求9个数据(x1、x2、……、x9 , 其平均数为m)的标准差S, 计算公式为:![]() ________;理由________
________;理由________
查看答案和解析>>
科目:初中数学 来源: 题型:
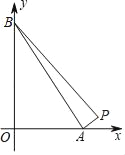
【题目】由点P(14,1),A(a,0),B(0,a)确定的△PAB的面积为18.
(1)如图,若0<a<14,求a的值.
(2)如果a>14,请画图并求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.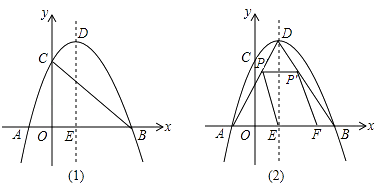
(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )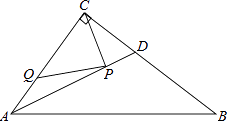
A.![]()
B.4
C.![]()
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com