
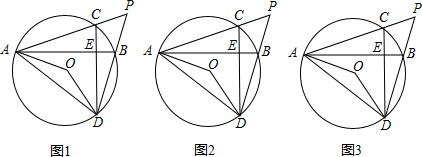
分析 (1)因为$\widehat{BC}=\widehat{BC}$,所以∠CAE=∠CDB,又∠AOD=2∠ACD,所以∠AOD=∠ACD+(∠CDB+∠P)=∠ACD+∠CAE+∠P=90°+∠P;
(2)延长AO交BD于点F,交CD于G,由于∠CAB+∠ACG=∠DGF+∠CDB,所以∠GFD=90°,所以AF垂直平分线段BD;
(3)利用∠AOD=90°+∠P,所以∠HBP=90°,由因为OA=AH=HB=5,所以由勾股定理可求得PH=$\frac{25}{4}$,所以tan∠PHB=tan∠BAD,设AE=4m,ED=3m,所以AB=AD=5m,EB=m,HM=$\frac{5}{6}m$,再利用勾股定理可求得m的值,求出AB和CD的长度后,利用四边形的面积为$\frac{1}{2}$AB•CD即可得答案.
解答 (1)证明:∵AB⊥CD,
∴∠AEC=90°,
∴∠CAE+∠ACD=90°
∵$\widehat{BC}=\widehat{BC}$,
∴∠CAE=∠CDB
∵$\widehat{AD}=\widehat{AD}$,
∴∠AOD=2∠ACD,
∵∠ACD=∠CDB+∠P
∴∠AOD=∠ACD+(∠CDB+∠P)=∠ACD+∠CAE+∠P=90°+∠P;
(2)如图1,延长AO交BD于点F,交CD于G,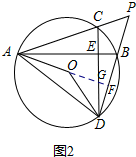
∵AB平分∠CAO,AB⊥CD,
∴AC=AG,
∴∠ACG=∠AGC,
∵∠AGC=∠DGF,∠CAB=∠CDB,
∴∠CAB+∠ACG=∠DGF+∠CDB,
∴∠GFD=90°,
由垂径定理可知:AF垂直平分线段BD,
∴AB=AD;
(3) 过点O作OM⊥AB于点M,交AC于点H,
过点O作OM⊥AB于点M,交AC于点H,
连接HB,
设∠CAB=α,
∴由(2)可知:∠CAB=∠BAO=∠DAO=α,
∴∠ACD=90°-α,∠PHB=2α,
∠AOD=2∠ACD=2(90°-α)=180°-2α,
由(1)可知:∠AOD=90°+∠P,
∴∠PHB+∠P=2α+∠P=2α+∠AOD-90°=90°,
由(2)可知:AH=AO,
由垂径定理可知:AH=HB,
∴HB=AO=5,
∵PB=$\frac{15}{4}$,
∴由勾股定理可知:PH=$\frac{25}{4}$,
∵∠PHB=∠DAB=2α,
∴tan∠PHB=tan∠DAB=$\frac{PB}{HB}$=$\frac{3}{4}$,
∴设AE=4m,ED=3m,
∴由勾股定理可知:AD=5m,
∵AB=AD=5m,
∴EB=5m-4m=m,
∵∠CDB=∠CAB,
∴tan∠CDB=tan∠BAO=$\frac{EB}{ED}$=$\frac{1}{3}$,
∵由垂径定理可知:AM=$\frac{1}{2}$AB=$\frac{5}{2}$m,
∴tan∠BAO=$\frac{OM}{AM}$,tan∠CAE=$\frac{CE}{AE}$,
∴OM=$\frac{5}{6}m$,CE=$\frac{4}{3}m$,
∴CD=$\frac{13}{3}$m,
∵由勾股定理可知:AO2=AM2+OM2,
∴52=($\frac{5}{2}$m)2+($\frac{5}{6}$m)2,
∴m=$\frac{3\sqrt{10}}{5}$,
∴四边形ACBD的面积为:$\frac{1}{2}$AB•CE+$\frac{1}{2}$AB•ED=$\frac{1}{2}$AB•CD=$\frac{65}{6}$m2=39.
点评 本题考查圆的综合问题,涉及圆周角定理,等量代换,垂径定理,勾股定理等知识,考查学生综合运用知识的能力.


科目:初中数学 来源: 题型:解答题
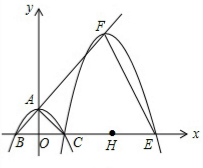 如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.
如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
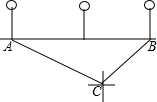 周末,小明一家去东昌湖划船,当船划到湖中C点处时,湖边的路灯A位于点C的北偏西64°方向上,路灯B位于点C的北偏东44°方向上,已知每两个路灯之间的距离是50米,求此时小明一家离岸边的距离是多少米?(精确到1米)(参考数据:
周末,小明一家去东昌湖划船,当船划到湖中C点处时,湖边的路灯A位于点C的北偏西64°方向上,路灯B位于点C的北偏东44°方向上,已知每两个路灯之间的距离是50米,求此时小明一家离岸边的距离是多少米?(精确到1米)(参考数据:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com