
【题目】随着地铁和共享单车的发展,“地铁![]() 单车”已成为很多市民出行的选择
单车”已成为很多市民出行的选择![]() 张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为
张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为![]() 单位:千米
单位:千米![]() ,乘坐地铁的时间为
,乘坐地铁的时间为![]() 单位分钟
单位分钟![]() ,经测量,得到如下数据:
,经测量,得到如下数据:
地铁站 | A | B | C | D |
| E |
| 6 |
| 10 | |
| 15 |
| 9 | 12 | a | 20 |
| b |
![]() 根据表中数据的规律,直接写出表格中a、b的值和
根据表中数据的规律,直接写出表格中a、b的值和![]() 关于x的函数表达式;
关于x的函数表达式;
![]() 张老师骑单车的时间
张老师骑单车的时间![]() 单位:分钟
单位:分钟![]() 也受x的影响,其关系可以用
也受x的影响,其关系可以用![]() 米描述,
米描述,
![]() 若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
![]() 若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
【答案】(1)![]() (2)张老师从学校回到家需要33分钟;故张老师应选择在C站出地铁,才能使他从学校回到家所需的时间最短,最短时间为25分钟.
(2)张老师从学校回到家需要33分钟;故张老师应选择在C站出地铁,才能使他从学校回到家所需的时间最短,最短时间为25分钟.
【解析】
![]() 由表中数据中距离每增加
由表中数据中距离每增加![]() 千米,时间增加3分钟,即每千米需要2分钟,据此可得a、b的值,再利用待定系数法求解可得
千米,时间增加3分钟,即每千米需要2分钟,据此可得a、b的值,再利用待定系数法求解可得![]() 关于x的函数表达式;
关于x的函数表达式;
![]() 设张老师从学校回到家所需时间为y分钟,则
设张老师从学校回到家所需时间为y分钟,则![]() ,求出
,求出![]() 时y的值即可;
时y的值即可;
![]() 由
由![]() ,利用二次函数的性质求解可得.
,利用二次函数的性质求解可得.
解:![]() 由表中数据中距离每增加
由表中数据中距离每增加![]() 千米,时间增加3分钟,
千米,时间增加3分钟,
即每千米需要2分钟,
则![]() 、
、![]() ,
,
设![]() ,
,
根据题意得:![]() ,
,
解得:![]() ,
,
所以![]() ;
;
![]() 设张老师从学校回到家所需时间为y分钟,
设张老师从学校回到家所需时间为y分钟,
则![]() ,
,
当![]() 时,
时,![]() ,
,
答:张老师从学校回到家需要33分钟.
![]() 由
由![]() ,
,
![]() 当
当![]() 时,y由最小值,最小值为25,
时,y由最小值,最小值为25,
故张老师应选择在C站出地铁,才能使他从学校回到家所需的时间最短,最短时间为25分钟.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的例题,范例:解方程![]() ,
,
解:(1)当![]() ≥0时,原方程化为
≥0时,原方程化为![]() ,解得:
,解得:![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
(2)当![]() <0时,原方程化为
<0时,原方程化为![]() ,解得:
,解得:![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
∴原方程的根是![]() ,
,![]()
请参照例题解方程![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△OAB是边长为2的等边三角形过点A的直线![]() 与
与![]() 轴交于点E,
轴交于点E,
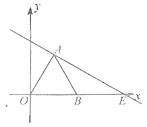
(1)求点E坐标。
(2)求过A,O,E三点的抛物线表达式。
(3)若P是(2)中求出的抛物线AE段上的一动点(不与A、E重合),设四边形OAPE的面积为S,求S的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中∠BAC=90°,D,E分别是AB,BC的中点,F在CA的延长线上∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 是关于
是关于![]() 的二次函数,求:
的二次函数,求:
![]() 求满足条件的
求满足条件的![]() 值;
值;
![]() 当抛物线开口向下时,请写出此时抛物线的顶点坐标;
当抛物线开口向下时,请写出此时抛物线的顶点坐标;
![]() 为何值时,抛物线有最小值?最小值是多少?当
为何值时,抛物线有最小值?最小值是多少?当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O 的内接四边形 ABCD 两组对边延长线分别交于点 E、F.
(1)若∠E=∠F,求证:∠ADC=∠ABC;
(2)若∠E=∠F=40°,求∠A 的度数;
(3)若∠E=30°,∠F=40°,求∠A 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好落在AB边上,连接AE. 求:
(1)旋转角的度数;
(2)AE的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com