
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 在线段
在线段![]() 上运动(D不与B、C重合),连接AD,作
上运动(D不与B、C重合),连接AD,作![]() ,
, ![]() 交线段
交线段![]() 于
于![]() .
.
(1)当![]() 时,
时, ![]() ____________°, ∠DEC ____________°;点D从B向C运动时,
____________°, ∠DEC ____________°;点D从B向C运动时, ![]() 逐渐变____________(填“大”或“小”);
逐渐变____________(填“大”或“小”);
(2)当![]() 等于多少时,
等于多少时, ![]() ≌
≌![]() ,请说明理由;
,请说明理由;
(3)在点D的运动过程中, ![]() 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出![]() 的度数.若不可以,请说明理由。
的度数.若不可以,请说明理由。

【答案】(1)25°,115°,小
(2)当![]() 等于2时,
等于2时, ![]() ≌
≌![]() .
.
(3) 80°或110°
【解析】分析:(1)首先利用三角形内角和为180°可算出∠BAD=180°-40°-115°=25°;再利用邻补角的性质和三角形内角和定理可得∠DEC的度数;
(2)当DC=2时,利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形.
本题解析:(1)∵∠B=40°,∠ADB=115°,
∴∠BAD=180°40°115°=25°;
∵∠ADE=40°,∠ADB=115°,
∴∠EDC=180°∠ADB∠ADE=180°115°40°=25°.
∴∠DEC=180°40°25°=115°,
当点D从B向C运动时,∠BDA逐渐变小;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
在△ABD和△DCE中,
 ,
,
∴△ABD≌△DCE(AAS);
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,
∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAC=70°°,
∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为80°时,
∴∠ADC=100°,
∵∠C=40°,
∴∠DAC=40°,
∴△ADE的形状是等腰三角形。


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
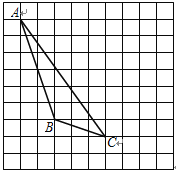
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不等式变形中,错误的是( )
A. 若 a≤b,则 a+c≤b+cB. 若 a+c≤b+c,则 a≤b
C. 若 a≤b,则 ac2≤bc2D. 若 ac2≤bc2,则 a≤b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大爷用280元买了甲、乙两种药材,甲种药材每千克20元,乙种药材每千克60元,且甲种药材比乙种药材多买了2千克,则甲种药材买了___千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】禽流感病毒的形状一般为球形,直径大约为0.000000102m,该直径用科学记数法表示为( )
A. 1.02×10﹣7mB. 10.2×10﹣7mC. 1.02×10﹣6mD. 1.0×10﹣8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 对角线互相平分的四边形是平行四边形
B. 对角线相等的四边形是矩形
C. 对角线互相垂直的四边形是菱形
D. 对角线互相垂直的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )(1)带根号的数都是无理数;(2)立方根等于本身的数是0和1;(3)﹣a一定没有平方根;(4)实数与数轴上的点是一一对应的;(5)两个无理数的差还是无理数.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com