
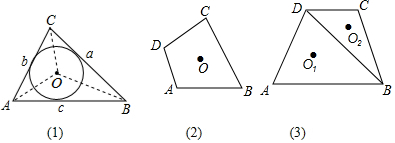
分析 (1)已知已给出示例,我们仿照例子,连接OA,OB,OC,OD,则四边形被分为四个小三角形,且每个三角形都以内切圆半径为高,以四边形各边作底,这与题目情形类似.仿照证明过程,r易得;
(2)(1)中已告诉我们内切圆半径的求法,如是我们再相比即得结果.但求内切圆半径需首先知道三角形各边边长,根据等腰梯形性质,过点D作AB垂线,进一步易得BD的长,则r1、r2、$\frac{{r}_{1}}{{r}_{2}}$易得.
解答  解:(1)如图,连接OA、OB、OC、OD,
解:(1)如图,连接OA、OB、OC、OD,
∵S=S△AOB+S△BOC+S△COD+S△AOD=$\frac{1}{2}$ar+$\frac{1}{2}$br+$\frac{1}{2}$cr+$\frac{1}{2}$dr=$\frac{1}{2}$(a+b+c)r,
∴r=$\frac{2S}{a+b+c+d}$;
(2)∵AB∥CD,
∴S△ABD:S△BCD=AB:CD=21:11;
∵r1=$\frac{2{S}_{△ABD}}{AB+BD+AD}$=$\frac{2{S}_{△ABD}}{54}$,
r2=$\frac{2{S}_{△CDB}}{CD+CB+DB}$=$\frac{2{S}_{△CDB}}{44}$,
∴$\frac{{r}_{1}}{{r}_{2}}$=$\frac{{S}_{△ABD}}{27}$:$\frac{{S}_{△BCD}}{22}$=$\frac{{S}_{△ABD}}{27}$×$\frac{22}{{S}_{△BCD}}$=$\frac{21×22}{27×11}$=$\frac{14}{9}$.
点评 本题考查了角平分线的定义,三角形面积计算以及等腰梯形等相关知识的综合应用,这类创新性题目已经成为新课标热衷的考点,同时要求学生在日常的学习中要注重自我学习能力的培养.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com