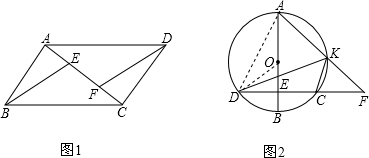
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵CE=AF,
∴CE-EF=AF-EF,
∴AE=CF,
在△ABE和△DCF中,
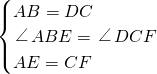
,
∴△ABE≌△DCF(SAS).
(2)①证明:连接AD,
∵∠CKF是圆内接四边形ADCK的外角,
∴∠CKF=∠ADC.
∵AB为⊙的直径,弦CD⊥AB,
∴弧AD=弧AC,
∴∠ADC=∠AKD,
∴∠AKD=∠CKF.
(2)解:连接OD.
∵AB为⊙的直径,AB=10,
∴OD=5,
∵弦CD⊥AB,CD=6,
∴DE=3,
在Rt△ODE中,OD=5,DE=3,由勾股定理得:OE=

=4,
∴AE=5+4=9,
在Rt△ADE中,tan∠CKF=tan∠ADE=
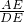
=
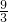
=3.
分析:(1)根据平行四边形性质得出AB=CD,AB∥CD,推出∠BAE=∠DCF,AE=CF,根据全等三角形的判定推出即可;
(2)①求出∠CKF=∠ADC,根据垂径定理求出∠AKD=∠ADC,即可得出答案;②求出OE,求出AE,求出∠ADE的正切,即可得出答案.
点评:本题考查了平行四边形性质,全等三角形的判定,圆内接四边形性质,垂径定理,勾股定理,锐角三角函数值等知识点的应用,主要考查学生的推理能力.

 上一动点,AK、DC的延长线相交于点F,连接CK、KD.
上一动点,AK、DC的延长线相交于点F,连接CK、KD.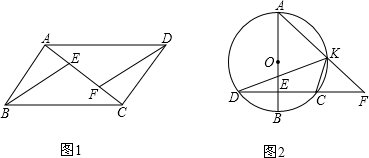
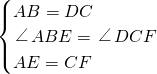 ,
,
 =4,
=4,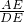 =
=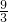 =3.
=3.

 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=