
 .质点P以4厘米/秒的速度,从点A出发沿线路A→B→D作匀速运动,质点Q以5厘米/秒的速度,从点D同时出发,沿线路D→C→B→A作匀速运动.
.质点P以4厘米/秒的速度,从点A出发沿线路A→B→D作匀速运动,质点Q以5厘米/秒的速度,从点D同时出发,沿线路D→C→B→A作匀速运动.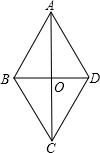

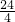 =6秒,PQ∥AD
=6秒,PQ∥AD  AB=60(厘米)
AB=60(厘米)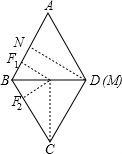


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
 (2013•赤峰)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(2013•赤峰)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠BAC=90°,将△ABC沿线段BC向右平移得到△DEF,使CE=AE,连结AD、AE、CD,则下列结论:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四边形AECD为菱形,其中正确的共有( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC沿线段BC向右平移得到△DEF,使CE=AE,连结AD、AE、CD,则下列结论:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四边形AECD为菱形,其中正确的共有( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com