
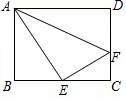
 如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则cos∠EAF=$\frac{7\sqrt{65}}{65}$.
如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则cos∠EAF=$\frac{7\sqrt{65}}{65}$. 分析 作点E关于直线CD的对称点E′,连接AE′交CD于点F,作EH⊥AF于H.,再根据△CEF∽△BEA即可求出CF的长,进而得出DF的长,想办法求出AE、AH,即可求出cos∠EAF的值.
解答 解:作点E关于直线CD的对称点E′,连接AE′交CD于点F,作EH⊥AF于H.
∵在矩形ABCD中,AB=6,BC=8,点E是BC中点,
∴BE=CE=CE′=4,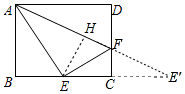
∵AB⊥BC,CD⊥BC,
∴$\frac{CE'}{BE'}=\frac{CF}{AB}$,即$\frac{4}{8+4}=\frac{CF}{6}$,解得CF=2,
∴DF=CD-CF=6-2=4.
∴AE=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$,AF=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∵S△AEF=$\frac{1}{2}$•AF•EH=S矩形ABCD-S△ABE-S△ADF-S△EFC,
∴$\frac{1}{2}$$•4\sqrt{5}$•EH=16,
∴EH=$\frac{8\sqrt{5}}{5}$,
在Rt△AEH中,AH=$\sqrt{A{E}^{2}-E{H}^{2}}$=$\sqrt{(2\sqrt{13})^{2}-(\frac{8\sqrt{5}}{5})^{2}}$=$\frac{14\sqrt{5}}{5}$,
∴cos∠EAF=$\frac{AH}{AE}$=$\frac{\frac{14\sqrt{5}}{5}}{2\sqrt{13}}$=$\frac{7\sqrt{65}}{65}$.
故答案为$\frac{7\sqrt{65}}{65}$.
点评 本题考查的是轴对称-最短路线问题、相似三角形的判定与性质、锐角三角函数等知识,解题的关键是学会利用对称解决最短问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
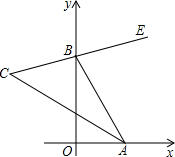 如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
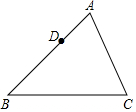 如图,已知锐角△ABC,点D是AB边上的一定点,请用尺规在AC边上求作一点E,使△ADE与△ABC相似.(作出符合题意的一个点即可,保留作图痕迹,不写作法.)
如图,已知锐角△ABC,点D是AB边上的一定点,请用尺规在AC边上求作一点E,使△ADE与△ABC相似.(作出符合题意的一个点即可,保留作图痕迹,不写作法.)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 二次函数y=ax2+bx+c的图象是过点A(-1,-$\frac{5}{2}$),B(0,-4),C(4,0)的一条抛物线.
二次函数y=ax2+bx+c的图象是过点A(-1,-$\frac{5}{2}$),B(0,-4),C(4,0)的一条抛物线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com