
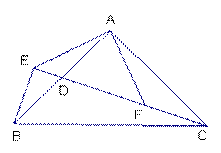
如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交 CD于点F.
CD于点F.
(1)求证:AE=AF; (2)求证:CD=2BE+DE.
(1)
∵∠BAC=90°, AF⊥AE
∴∠EA B+∠BAF=∠BA
B+∠BAF=∠BA F+∠FAC=90°
F+∠FAC=90°
∴∠EAB=∠FAC
∵BE⊥CD
∴∠BEC=90°
∴∠EBD+∠EDB=∠ADC+∠ACD=90°
∵∠EDB=∠ADC
∴∠ EBD =∠ACD
EBD =∠ACD
∵AB=AC
∴△AEB≌△AFC
∴ AE=A F
F
(2)
作AG⊥EC,垂足为G
∵AG⊥EC, BE⊥CD
∴∠BED=∠AGD=90°
∵点是AB的中点
∴BD=AD
∵∠BED=∠AGD
∴△BED≌△AGD
∴ED=GD,BE=AG
∵AE=AF
∴∠AEF=∠AFE=45°
∴∠FAG=45°
∴∠GAF=∠GFA
∴GA=GF
∴CF=BE=AG=GF
∵CD=DG+GF+FC
∴CD=DE+BE+BE
∴CD=2BE+DE


科目:初中数学 来源: 题型:
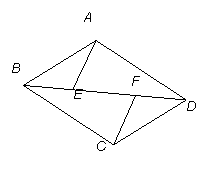
如图,已知AB=DC,AD=BC,E,F在DB上两点且BF=DE,若∠AEB=120°,
∠ADB=30°,则∠BCF= ( )[
 A.150° B.40° C.80° D.90°
A.150° B.40° C.80° D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
(1) 特殊情况•探索结论:当点E为AB的中点时,如图1,确定线段AE与的
DB大小关系.请你直接写出结论:AE DB(填“>”,“<”或“=”).
(2)特例启发,解答題目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由
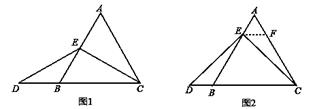 如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ ABC
的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点E、F分别是□ABCD的边BC、AD上的点,且BE=DF.
(1) 求证:四边形AECF是 平行四边形;
平行四边形;
(2) 若AE=BE,∠BAC=90°,试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com