
【题目】问题背景:
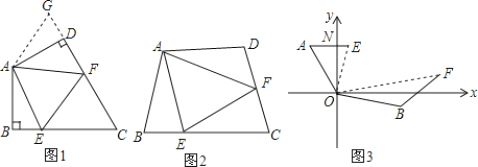
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠D=90°.E、F分别是BC、CD上的点,且∠EAF=60°.为了探究图中线段BE,EF,FD之间的数量关系,小红的想法是:在EB的延长线上取一点G,使得BG=DF,连接AG,证明△ABG≌△ADF;再证明△AGE≌△AFE,从而得到结论,她的结论是_____________.
探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西40°的A处,舰艇乙在指挥中心南偏东80°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以50海里/小时的速度,同时舰艇乙沿北偏东50°的方向以70海里/小时的速度各自前进2小时后,在指挥中心观测到甲、乙两舰艇分别到达E,F处,两舰艇与指挥中心之间的夹角为70°,则此时两舰艇之间的距离为______海里.
【答案】问题背景:EF=BE+DF;探索延伸:EF=BE+DF仍然成立;实际应用:240海里.
【解析】
问题背景:延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
探索延伸:延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
结论应用:连接EF,延长AE、BF相交于点C,然后与(2)同理可证;
解:问题背景:EF=BE+DF,证明如下:
在△ABE和△ADG中,
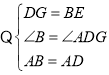
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,

∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF;
探索延伸:结论EF=BE+DF仍然成立;
理由:延长FD到点P.使DP=BE.连结AP,如图2,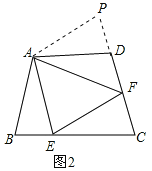
在△ABE和△ADP中,
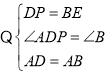
∴△ABE≌△ADP(SAS),
∴AE=AP,∠BAE=∠DAP,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠PAF=∠DAP+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠PAF,
在△AEF和△PAF中,

∴△AEF≌△APF(SAS),
∴EF=FP,
∵FP=DP+DF=BE+DF,
∴EF=BE+DF;
结论应用:如图3,连接EF,延长AE、BF相交于点C,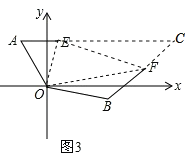
∵∠AOB=40°+90°+(90°-80°)=140°,∠EOF=70°,
∴∠EOF=![]() ∠AOB,
∠AOB,
又∵OA=OB,∠OAC+∠OBC=(90°-40°)+(80°+50°)=180°,
∴符合探索延伸中的条件,
∴结论EF=AE+BF成立,
即EF=2×(50+70)=240海里.
答:此时两舰艇之间的距离是240海;


科目:初中数学 来源: 题型:
【题目】某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元

(1)若他选择转动转盘1,则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt![]() 中,∠BAC=90°且AB=AC,D是边BC上一点,E是边AC上一点,AD=AE,若
中,∠BAC=90°且AB=AC,D是边BC上一点,E是边AC上一点,AD=AE,若![]() 为等腰三角形,则∠CDE的度数为____________
为等腰三角形,则∠CDE的度数为____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数![]() 之间的一种运算,记作(
之间的一种运算,记作(![]() );如果
);如果![]() ,那么(
,那么(![]() )
)![]() ,例如因为
,例如因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:(4,16)= ,(7,1)= ,( ,81)=4.
(2)小明在研究这种运算时发现一个现象,(![]() ,
,![]() )=(3,4),小明给出了如下的证明:
)=(3,4),小明给出了如下的证明:
设(![]() ,
,![]() )
)![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
即(3,4)![]() ,所以(
,所以(![]() ,
,![]() )=(3,4),请你尝试运用这种方法解决下列问题:
)=(3,4),请你尝试运用这种方法解决下列问题:
①证明:(6,45)-(6,9)=(6,5)
②猜想:(![]() ,
,![]() )+(
)+(![]() ,
,![]() )=( , )(结果化成最简形式)
)=( , )(结果化成最简形式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用棋子摆成的“上”字:

第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和 枚棋子.
(2)第n个“上”字需用 枚棋子.
(3)如果某一图形共有102枚棋子,你知道它是第几个“上”字吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com