【题目】下面四个整式中，不能表示图中阴影部分面积的是（ ）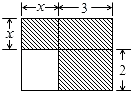
A.（x+3）（x+2）﹣2x
B.x（x+3）+6
C.3（x+2）+x2
D.x2+5x
【答案】D
【解析】解：A、大长方形的面积为：（x+3）（x+2），空白处小长方形的面积为：2x，所以阴影部分的面积为（x+3）（x+2）﹣2x，故正确；
B、阴影部分可分为两个长为x+3，宽为x和长为x+2，宽为3的长方形，他们的面积分别为x（x+3）和3×2=6，所以阴影部分的面积为x（x+3）+6，故正确；
C、阴影部分可分为一个长为x+2，宽为3的长方形和边长为x的正方形，则他们的面积为：3（x+2）+x2 ， 故正确；
D、x2+5x，故错误；
故选D．
根据题意可把阴影部分分成两个长方形或一个长方形和一个正方形来计算面积，也可以用大长方形的面积减去空白处小长方形的面积来计算．
科目：初中数学 来源： 题型：
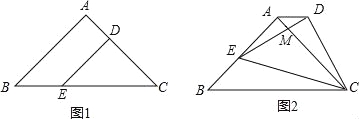
【题目】如图1，在△ABC中，∠BAC=90°，AB=AC=2
，D、E两点分别在AC、BC上，且DE∥AB，DC=2
，将△CDE绕点C顺时针旋转得到△CD′E′，如图2，点D、E对应点分别为D′、E′、D′、E′与AC相交于点M，当E′刚好落在边AB上时，△AMD′的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
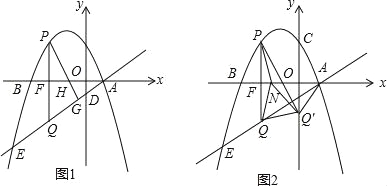
【题目】如图1，抛物线y=﹣
x2﹣
x+3与x轴交于A、B两点（点A在点B的右侧），交y轴于点C，点D的坐标为（0，﹣1），直线AD交抛物线于另一点E，点P是第二象限抛物线上的一点，作PQ∥y轴交直线AE于Q，作PG⊥AD于G，交x轴于点H
（1）求线段DE的长；
（2）设d=PQ﹣
PH，当d的值最大时，在直线AD上找一点K，使PK+
EK的值最小，求出点K的坐标和PK+EK的最小值；
（3）如图2，当d的值最大时，在x轴上取一点N，连接PN，QN，将△PNQ沿着PN翻折，点Q的对应点为Q′，在x轴上是否存在点N，使△AQQ′是等腰三角形？若存在，求出点N的坐标，若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果M个不同的正整数，对其中的任意两个数，这两个数的积能被这两个数的和整除，则称这组数为M个数的祖冲之数组．如（3，6）为两个数的祖冲之数组，因为3×6能被（3+6整除）；又如（15，30，60）为三个数的祖冲之数组，因为（15×30）能被（15+30）整除，（15×60）能被（15+60）整除，（30×60）能被（30+60）整除…
（1）我们发现，3和6，4和12，5和20，6和30…，都是两个数的祖冲之数组；由此猜测n和n（n﹣1）（n≥2，n为整数）组成的数组是两个数的祖冲之数组，请证明这一猜想．
（3）若（4a，5a，6a）是三个数的祖冲之数组，求满足条件的所有三位正整数a．
查看答案和解析>>
科目：初中数学 来源： 题型：
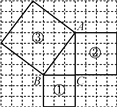
【题目】如图，正方形网格中，每个小正方形的边长都为 1.
(1)正方形①的面积 S1＝_________cm2 ，正方形②的面积 S2＝______________cm2，正方形③的面积S3＝____cm2；
(2)S1,S2,S3之间存在什么关系？
(3)猜想：如果Rt△ABC的三边BC，AC，AB的长分别为a,b,c,那么它们之间存在什么关系？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com