
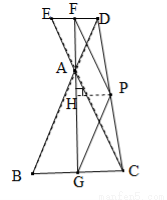
△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α (0°<α ≤90°) ,点F,G,P分别是DE,BC,CD的中点,连接PF,PG.
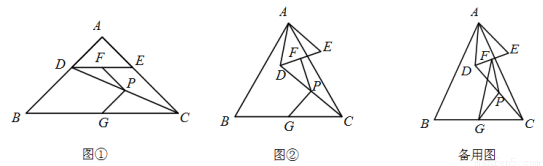
(1)如图①,α=90°,点D在AB上,则∠FPG= °;
(2)如图②,α=60°,点D不在AB上,判断∠FPG的度数,并证明你的结论;
(3)连接FG,若AB=5, AD=2,固定△ABC,将△ADE绕点A旋转,当PF的长最大时,FG的长为 (用含α的式子表示).
(1)90°;(2)120°,证明见试题解析;(3)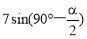 (也可以写成
(也可以写成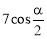 ).
).
【解析】
试题分析:(1)由AB=AC、AD=AE,得BD=CE,再根据G、P、F分别是BC、CD、DE的中点,可得出PG∥BD,PF∥CE.则∠GPF=180°﹣∠α=90°;
(2)连接BD,连接CE,由已知可证明△ABD≌△ACE,则∠ABD=∠ACE.因为G、P、F分别是BC、CD、DE的中点,则PG∥BD,PF∥CE.进而得出∠GPF=180°﹣∠α=120°;
(3)当D在BA的延长线上时,CE=BD最长,此时BD=AB+AD=5+2=7,再由三角形中位线定理即可算出PG=3.5,在Rt△GPH中,由三角函数的定义即可求出GH,进一步求出FG.
试题解析:(1)∵AB=AC、AD=AE,∴BD=CE,∵G、P、F分别是BC、CD、DE的中点,∴PG∥BD,PF∥CE.∴∠ADC=∠DPG,∠DPF=∠ACD,∠GPF=∠DPF+∠DPG=∠ADC+∠ACD=180°﹣∠BAC=180°﹣∠α=90°,即∠GPF=90°;
(2)∠FPG=120°;理由:连接BD,连接CE.∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵G、P、F分别是BC、CD、DE的中点,∴PG∥BD,PF∥CE.∴∠PGC=∠CBD,∠DPF=∠DCE=∠DCA+∠ACE=∠DCA+∠ABD,∠DPG=∠PGC+∠BCD=∠CBD+∠BCD,∠GPF=∠DPF+∠DPG=∠DCA+∠ABD+∠CBD+∠BCD=180°﹣∠BAC=180°﹣∠α=120°,即∠GPF==120°;

(3)连结BD,CE,过P作PH⊥FG于H,由(2)可知,△ABD≌△ACE,∴BD=CE,且PG=PF=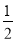 BD,当D在BA的延长线上时,CE最长,即BD最长,此时BD=AB+AD=5+2=7,∴PG=3.5,∵PF=PG,PH⊥FG,∴∠GPH=
BD,当D在BA的延长线上时,CE最长,即BD最长,此时BD=AB+AD=5+2=7,∴PG=3.5,∵PF=PG,PH⊥FG,∴∠GPH=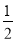 ∠FPG=
∠FPG=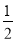 (180°﹣∠α)=90°﹣
(180°﹣∠α)=90°﹣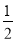 α,FG=2HG,∴FG=2HG=2PG•sin∠GPH=2×3.5×
α,FG=2HG,∴FG=2HG=2PG•sin∠GPH=2×3.5× =
=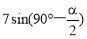 .
.
考点:1.旋转的性质;2.全等三角形的判定与性质;3.等腰三角形的性质;4.等边三角形的性质.


科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:解答题
某工厂设计了一款产品,成本为每件20元.投放市场进行试销,经调查发现,该种产品每天的销售量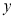 (件)与销售单价
(件)与销售单价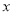 (元)之间满足
(元)之间满足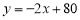 (20≤
(20≤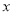 ≤40),设销售这种产品每天的利润为W(元).
≤40),设销售这种产品每天的利润为W(元).
(1)求销售这种产品每天的利润W(元)与销售单价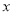 (元)之间的函数表达式;
(元)之间的函数表达式;
(2)当销售单价定为多少元时, 每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:选择题
以下事件为必然事件的是( )
A.掷一枚质地均匀的骰子,向上一面的点数是0
B.多边形的内角和是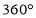
C.二次函数的图象必过原点
D.半径为2的圆的周长是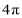
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市大兴区九年级上学期期末考试数学试卷(解析版) 题型:填空题
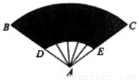
如图,扇形纸扇完全打开后,外侧两竹条AB,AC夹角为120°,AB的长为30cm,贴纸(阴影)部分BD的长为20cm,则贴纸部分的面积等于 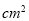 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市大兴区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠AOC等于( )

A.25° B.30° C.50° D.65°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市朝阳区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知关于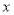 的一元二次方程
的一元二次方程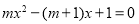 .
.
(1)求证:此方程总有两个实数根;
(2)若 为整数,当此方程的两个实数根都是整数时,求
为整数,当此方程的两个实数根都是整数时,求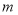 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市朝阳区九年级上学期期末考试数学试卷(解析版) 题型:填空题
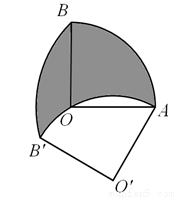
如图,在扇形OAB中,∠AOB=90°,OA=3,将扇形OAB绕点A逆时针旋转n°(0<n<180)后得到扇形O′AB′ ,当点O在弧AB'上时,n为 ,图中阴影部分的面积为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市昌平区九年级上学期期末考试数学试卷(解析版) 题型:解答题
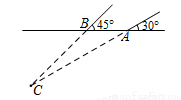
如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市七年级上学期期末考试数学试卷(解析版) 题型:选择题
未来三年,我国将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿
用科学记数法表示为( ).
A.0.845×104亿元 B.8.45×103亿元
C.8.45×104亿元 D.84.5×102亿元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com