Question

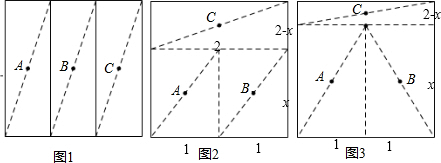
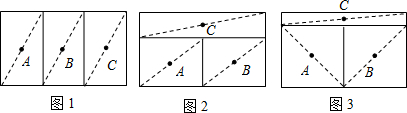
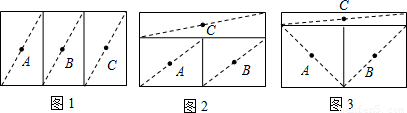
三个牧童A，B，C在一块正方形的牧场上看守一群牛，为保证公平合理，他们商量将牧场划分为三块分别看守，划分的原则是：①每个人看守的牧场面积相等；②在每个区域内，各选定一个看守点，并保证在有情况时他们所需走的最大距离（看守点到本区域内最远处的距离）相等．按照这一原则，他们先设计了一种如图1的划分方案：把正方形牧场分成三块全等的长方形，大家分头守在这三个长方形的中心（对角线交点），看守自己的一块牧场．
过了一段时间，牧童B和牧童C又分别提出里新的划分方案．
牧童B的划分方案如图2：三块长方形的面积相等，牧童的位置在三个小长方形的中心．
牧童C的划分方案如图3：把正方形的牧场分成三块长方形，牧童的位置在三个小长方形的中心，并保证在有情况时三个人所需走的最大距离相等．请回答：

（I）长方形的两条对角线是相等且互相平分的吗？
（II）牧童B的划分方案中，哪个牧童在有情况时所需走的最大距离较远？
（III）牧童C的划分方案是否符合他们商量的划分原则？为什么？（提示：在计算时可取正方形边长为2）

Answer 1

分析：（I）根据长方形的性质即可得到长方形的两条对角线是相等且互相平分．
（II）设正方形牧场的边长为2，牧童A和B看守的长方形的一边为1，设另一边为x，根据三块长方形的面积相等，有牧童B所在长方形的面积等于正方形面积的三分一，即

1

2

x=

1

3

×2²，解出x=

4

3

，然后根据勾股定理分别计算出牧童A和B所需走的最大距离和牧童C所需走的最大距离，再比较大小即可得到谁走的最大距离较远；
（III）设正方形牧场的边长为2，对于牧童C的划分方案，牧童A和B看守的长方形的一边为1，设另一边为x，根据三个人所需走的最大距离相等，利用勾股定理得到
1²+x²=2²+（2-x）²，解得x=

7

4

，然后计算牧童B所在长方形的面积为

7

4

，它不等于正方形面积的三分一，因此得到牧童C的划分方案不符合他们商量的划分原则．

解答：解：（I）长方形的两条对角线是相等且互相平分．
（II）设正方形牧场的边长为2，对于牧童B的划分方案，如图2：牧童A和B看守的长方形的一边为1，设另一边为x，
∵三块长方形的面积相等，
∴

1

2

x=

1

3

×2²，x=

4

3

，
∴牧童A和B所需走的最大距离为长方形的对角线长的一半：

1

2

12+( 4 3 )2

=

5

6

，牧童C所需走的最大距离为：

1

2

2 2+(2- 4 3 )2

=

10

3

，
∴牧童C在有情况时所需走的最大距离较远．
（III）牧童C的划分方案不符合他们商量的划分原则．理由如下：
设正方形牧场的边长为2，对于牧童C的划分方案，如图3：牧童A和B看守的长方形的一边为1，设另一边为x，
∵三个人所需走的最大距离相等，
∴1²+x²=2²+（2-x）²，解得x=

7

4

，
∴牧童B的所在的长方形的面积=1×

7

4

=

7

4

，而正方形面积的三分之一为

4

3

，
∴三个长方形的面积不相等，不符合他们商量的划分原则．

点评：本题考查了正方形的性质：正方形的四边相等，四个角都为90°，面积等于边长的平方．也考查了长方形的性质以及勾股定理．