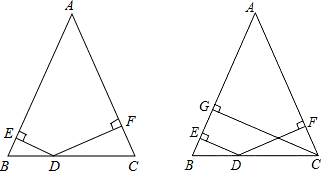
(1)当点D在BC的中点上时,DE=DF,
证明:∵D为BC中点,
∴BD=CD,
∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
∵在△BED和△CFD中
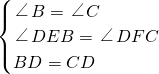
,
∴△BED≌△CFD(AAS),
∴DE=DF.
(2)解:
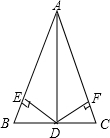
有3对全等三角形,有△BED≌△CFD,△ADB≌△ADC,△AED≌△AFD,
∵由(1)知△BED≌△CFD,
∴DE=DF,BE=CF,
∵AB=AC,
∴AE=AF,
在△AED和△AFD中
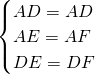
,
∴△AED≌△AFD(SSS),
∵在△ADB和△ADC中
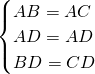
∴△ADB≌△ADC(SSS),
∴有3对全等三角形,有△BED≌△CFD,△ADB≌△ADC,△AED≌△AFD;
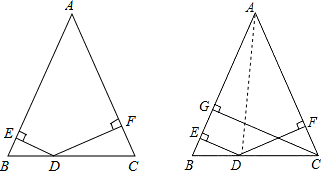
(3)CG=DE+DF
证明:连接AD,
∵S
三角形ABC=S
三角形ADB+S
三角形ADC,
∴

AB×CG=

AB×DE+

AC×DF,
∵AB=AC,
∴CG=DE+DF.
分析:(1)根据AAS证△BED≌△CFD,根据全等三角形的性质推出即可;
(2)求出DE=DF,AE=AF,根据SSS证出△AED≌△AFD即可,根据SSS证出△ABD≌△ACD即可;
(3)连接AD,根据三角形的面积公式求出即可.
点评:本题考查了全等三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力.

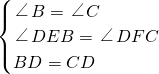 ,
,
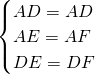 ,
,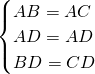

 AB×CG=
AB×CG= AB×DE+
AB×DE+ AC×DF,
AC×DF,

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为