
���� ��1�����ݡ����ÿ����Ʒÿ����1Ԫ��ÿ���ڿɶ�����10������֪������Ϊ��500+10��50-x������42��x��50�������ݡ����ÿ����Ʒÿ�Ǽ�1Ԫ����ÿ����������5������֪������Ϊ��500-5��x-50������50��x��70����
��2����������=������������������ֽ��ۺ��Ǽ��г�w��x�ĺ�����ϵʽ��
��3����42��x��50��50��x��70�ֱ������������ֵ������⣮
��� �⣺��1�������ÿ����Ʒÿ����1Ԫ��ÿ���ڿɶ�����10����
����������500+10��50-x��=-10x+1000��42��x��50����
�����ÿ����Ʒÿ�Ǽ�1Ԫ����ÿ����������5����
����������500-5��x-50��=-5x+750��50��x��70����
��y=$\left\{\begin{array}{l}{-10x+100��42��x��50��}\\{-5x+750��50��x��70��}\end{array}\right.$��
��2������ʱ��W=��x-40����-10x+1000��=-10x2+1400x-40000��42��x��50����
�Ǽ�ʱ��W=��x-40����-5x+750��=-5x2+950x-30000��50��x��70����
��W=$\left\{\begin{array}{l}{-10x2+1400x-40000��42��x��50��}\\{-5x2+950x-30000��50��x��70��}\end{array}\right.$��
��3����42��x��50ʱ��W=-10x2+1400x-40000=-10��x-70��2+9000
��x��70ʱ��W��x�����������
���Ե�x=50ʱ��W���W���=5000��
��50��x��70ʱ��W=-5x2+950x-30000=-5��x-95��2+15125��
��x��95ʱ��W��x�����������
���Ե�x=70ʱ��W���W���=12000��
���Ե�����Ʒ���ۼ۶�Ϊ70Ԫʱ������ʹÿ��������������������12000Ԫ��
���� ������Ҫ�����˶��κ�����ʵ��Ӧ�ã���ȷ��������ȷ����ͬ��Χ�ڵĺ�������ʽ�ǽ������Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
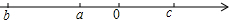 ʵ��a��b��c�������ϵĶ�Ӧ����ͼ��ʾ������|a|+|c-b|-|a+b|+|a-c|��
ʵ��a��b��c�������ϵĶ�Ӧ����ͼ��ʾ������|a|+|c-b|-|a+b|+|a-c|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�ı߳���4��E��AB��һ�㣬F��AD�ӳ����ϵ�һ�㣬BE=DF���ı���AEGF�Ǿ��Σ�����AEGF�����y��BE�ij�x�ı仯���仯��y��x֮��Ĺ�ϵ�����������ĺ�������ʾ��
��ͼ��������ABCD�ı߳���4��E��AB��һ�㣬F��AD�ӳ����ϵ�һ�㣬BE=DF���ı���AEGF�Ǿ��Σ�����AEGF�����y��BE�ij�x�ı仯���仯��y��x֮��Ĺ�ϵ�����������ĺ�������ʾ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com