
【题目】如图,在平面直角坐标系中,![]() 与
与![]() 轴相切,直线
轴相切,直线![]() 被
被![]() 截得的弦
截得的弦![]() 长为
长为![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则
,则![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
过点P作PH⊥AB于H,PD⊥x轴于D,交直线y=x于E,连结PA,根据切线的性质得PC⊥y轴,则P点的横坐标为4,所以E点坐标为(4,4),易得△EOD和△PEH都是等腰直角三角形,根据垂径定理由PH⊥AB得AH=![]() ,根据勾股定理可得PH=2,于是根据等腰直角三角形的性质得PE=
,根据勾股定理可得PH=2,于是根据等腰直角三角形的性质得PE=![]() ,则PD=
,则PD=![]() ,然后利用第一象限点的坐标特征写出P点坐标.
,然后利用第一象限点的坐标特征写出P点坐标.
解:过点P作PH⊥AB于H,PD⊥x轴于D,交直线y=x于E,连结PA,
∵⊙P与y轴相切于点C,
∴PC⊥y轴,
∴P点的横坐标为4,
∴E点坐标为(4,4),
∴△EOD和△PEH都是等腰直角三角形,
∵PH⊥AB,
∴AH=![]() ,
,
在△PAH中,PH=![]() ,
,
∴PE=![]() ,
,
∴PD= ![]() ,
,
∴P点坐标为(4,![]() ).
).
故选:B


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=12,点E在AD边上,且AE=8,EF⊥BE交CD于F.
(1)求证:△ABE∽△DEF;
(2)求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义一种新函数:形如![]() 的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数
的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是
时,函数的最小值是![]() ;⑤当
;⑤当![]() 时,函数的最大值是
时,函数的最大值是![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,抛物线与直线
,抛物线与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的解析式;
(2)坐标轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形?若存在,请直接写出点
为底边的等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)![]() 点在
点在![]() 轴上且位于点
轴上且位于点![]() 的左侧,若以
的左侧,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 的坐标分别
的坐标分别![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点的抛物线
为顶点的抛物线![]() 过点
过点![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向点
向点![]() 匀速运动,过点
匀速运动,过点![]() 作
作![]() 轴,交对角线
轴,交对角线![]() 于点
于点![]() .设点
.设点![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
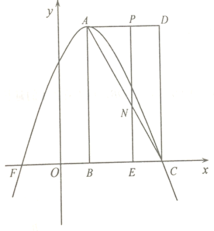
(1)求抛物线的解析式;
(2)若![]() 分
分![]() 的面积为
的面积为![]() 的两部分,求
的两部分,求![]() 的值;
的值;
(3)若动点![]() 从
从![]() 出发的同时,点
出发的同时,点![]() 从
从![]() 出发,以每秒1个单位的速度沿线段
出发,以每秒1个单位的速度沿线段![]() 向点
向点![]() 匀速运动,点
匀速运动,点![]() 为线段
为线段![]() 上一点.若以
上一点.若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形,求
为顶点的四边形为菱形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.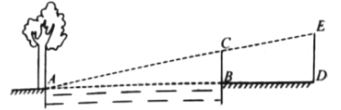
查看答案和解析>>
科目:初中数学 来源: 题型:
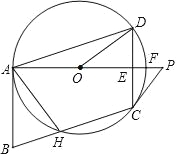
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小蓉从格致楼底楼点A处沿立人大礼堂旁的台阶AB拾阶而上,步行20米后到达万象楼楼底点B,再从点B直线行进15米到达直通博雅楼的台阶底端C,然后沿台阶CD步行至博雅楼底楼的小平台D.在D点处测得竖立于百汇园旁的万象楼BE的楼顶点E的仰角为30°.如图所示,已知台阶AB与水平地面夹角为45°,台阶CD与水平地面夹角为60°,CD=12米,点A,B,C,D,E在同一平面.则格致楼楼底点A到万象楼楼顶点E的垂直高度约为( )(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
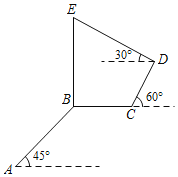
A.22.1米B.35.2米C.27.3米D.36.1米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com