
【题目】如图,正方形ABCD 中,AB=4,E为CD上一动点,连接AE交BD于F,过F作FH⊥AE于F,过H 作HG⊥BD 于 G.则下列结论:①AF=FH;②∠HAE=45°;③BD=2FG;④△CEH 的周长为 8.其中正确的个数是( )

A.1个B.2个C.3个D.4个
【答案】D
【解析】
①作辅助线,延长HF交AD于点L,连接CF,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;
②由FH⊥AE,AF=FH,可得:∠HAE=45°;
③作辅助线,连接AC交BD于点O,证BD=2FG,只需证OA=GF即可,根据△AOF≌△FGH,可证OA=GF,故可证BD=2FG;
④作辅助线,延长AD至点M,使AD=DM,过点C作CI∥HL,则IL=HC,可证AL=HE,再根据△MEC≌△MIC,可证:CE=IM,故△CEH的周长为边AM的长.
①连接FC,延长HF交AD于点L,

∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°.
∵AD=CD,DF=DF,
∴△ADF≌△CDF.
∴FC=AF,∠ECF=∠DAF.
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°.
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC.
∴FH=AF.
②∵FH⊥AE,FH=AF,
∴∠HAE=45°.
③连接AC交BD于点O,可知:BD=2OA,

∵∠AFO+∠GFH=∠GHF+∠GFH,
∴∠AFO=∠GHF.
∵AF=HF,∠AOF=∠FGH=90°,
∴△AOF≌△FGH.
∴OA=GF.
∵BD=2OA,
∴BD=2FG.
④连接EM,延长AD至点M,使AD=DM,过点C作CI∥HL,则:LI=HC,
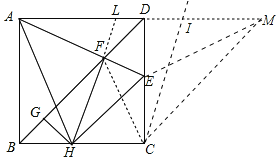
∵HL⊥AE,CI∥HL,
∴AE⊥CI,
∴∠DIC+∠EAD=90°,
∵∠EAD+∠AED=90°,
∴∠DIC=∠AED,
∵ED⊥AM,AD=DM,
∴EA=EM,
∴∠AED=∠MED,
∴∠DIC=∠DEM,
∴∠CIM=∠CEM,
∵CM=MC,∠ECM=∠CMI=45°,
∴△MEC≌△CIM,可得:CE=IM,
同理,可得:AL=HE,
∴HE+HC+EC=AL+LI+IM=AM=8.
∴△CEH的周长为8,为定值.
故①②③④结论都正确.
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )

A. 24m B. 25m C. 28m D. 30m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
(1)求证:BF=CF;
(2)若AB=2,AD=4,且∠AFC=2∠D,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料
在数轴上4与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]()
在数轴上![]() 与3所对的两点之间的距离
与3所对的两点之间的距离![]() ;
;
在数轴上![]() 与
与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]() 在数轴上点A、B分别表示数a、b,则A、B两点之间的距离
在数轴上点A、B分别表示数a、b,则A、B两点之间的距离![]()
依据材料知识解答下列问题
![]() 数轴上表示
数轴上表示![]() 和
和![]() 的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______;
的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______;
![]() 七年级研究性学习小组进行如下探究:
七年级研究性学习小组进行如下探究:
![]() 请你在草稿纸上面出数轴当表示数x的点在
请你在草稿纸上面出数轴当表示数x的点在![]() 与2之间移动时,
与2之间移动时,![]() 的值总是一个固定的值为:______,式子
的值总是一个固定的值为:______,式子![]() 的最小值是______.
的最小值是______.
![]() 请你在草稿纸上画出数轴,当x等于______时,
请你在草稿纸上画出数轴,当x等于______时,![]() 的值最小,且最小值是______.
的值最小,且最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察由棱长为 ![]() 的小立方体摆成的图形,寻找规律:如图 ① 中,共有
的小立方体摆成的图形,寻找规律:如图 ① 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ② 中,共有
个看不见;如图 ② 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;如图 ③ 中,共有
个看不见;如图 ③ 中,共有 ![]() 个小立方体,其中
个小立方体,其中 ![]() 个看得见,
个看得见, ![]() 个看不见;
个看不见; ![]() ,则第 ⑥个图中,看得见的小立方体有________________个.
,则第 ⑥个图中,看得见的小立方体有________________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某保温杯专卖店通过市场调研,准备销售![]() 、
、![]() 两种型号的保温杯,其中每件
两种型号的保温杯,其中每件![]() 种保温杯的进价比
种保温杯的进价比![]() 种保温杯的进价高20元,已知专卖店用3200元购进
种保温杯的进价高20元,已知专卖店用3200元购进![]() 种保温杯的数量与用2560元购进
种保温杯的数量与用2560元购进![]() 种保温杯的数量相同.
种保温杯的数量相同.
(1)求两种保温杯的进价;
(2)若![]() 种保温杯的售价为250元,
种保温杯的售价为250元,![]() 种保温杯的售价为180元,专卖店共进两种保温杯200个,设
种保温杯的售价为180元,专卖店共进两种保温杯200个,设![]() 种保温杯进货
种保温杯进货![]() 个,求该专卖店获得的总利润
个,求该专卖店获得的总利润![]() (元)与
(元)与![]() 种保温杯进货数
种保温杯进货数![]() (个)之间的函数关系式,并写出自变量的取值范围.
(个)之间的函数关系式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从![]() 地出发,匀速驶向
地出发,匀速驶向![]() 地.甲车以
地.甲车以![]() 的速度行驶
的速度行驶![]() 后,乙车才沿相同路线行驶.乙车先到达
后,乙车才沿相同路线行驶.乙车先到达![]() 地并停留
地并停留![]() 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离
后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离![]() 与乙车行驶时间
与乙车行驶时间![]() 之间的函数关系如图所示.下列说法:①乙车的速度是
之间的函数关系如图所示.下列说法:①乙车的速度是![]() ;②
;②![]() ;③点
;③点![]() 的坐标是
的坐标是![]() ;④
;④![]() .其中说法正确的是_________.
.其中说法正确的是_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com