
【题目】如图,抛物线![]() 过
过![]() 、
、![]() 两点,点
两点,点![]() 、
、![]() 关于抛物线的对称轴对称,过点
关于抛物线的对称轴对称,过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .
.
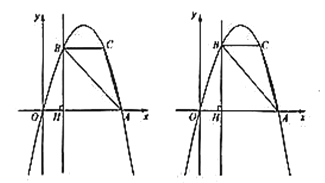
(1)求抛物线的解析式;
(2)直接写出![]() 点坐标,并求
点坐标,并求![]() 的面积;
的面积;
(3)点![]() 为抛物线上一动点,且位于第四象限,当
为抛物线上一动点,且位于第四象限,当![]() 面积为6时,求出
面积为6时,求出![]() 点坐标;
点坐标;
(4)若点![]() 在直线
在直线![]() 上运动,点
上运动,点![]() 在
在![]() 轴上运动,当以
轴上运动,当以![]() 、
、![]() 、
、![]() 为顶点的三角形为等腰直角三角形时,直接写出此时点
为顶点的三角形为等腰直角三角形时,直接写出此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,3;(3)
,3;(3)![]() ;(4)
;(4)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)把![]() 、
、![]() 代入
代入![]() ,得到关于a,b的二元一次方程组,求出a,b的值,即可得到抛物线的函数解析式;
,得到关于a,b的二元一次方程组,求出a,b的值,即可得到抛物线的函数解析式;
(2)根据抛物线的对称性,可得点C的坐标,从而可得BC的值以及BC边上的高,进而求出![]() 的面积;
的面积;
(3)设![]() ,作
,作![]() 于点
于点![]() ,由
,由![]() ,可列出关于m的方程,进而可求出点P的坐标;
,可列出关于m的方程,进而可求出点P的坐标;
(4)根据以点C,M,N为顶点的三角形为等腰直角三角形,分五类情况讨论,即可求解.
(1)∵抛物线![]() 过
过![]() 、
、![]() 两点,
两点,
∴![]() ,解得:
,解得:![]()
∴抛物线的解析式是:![]() .
.
(2)∵抛物线的解析式是:![]() ,
,
∴抛物线的对称轴是直线x=2,
∵点![]() 、
、![]() 关于抛物线的对称轴对称,点B的坐标是(1,3),
关于抛物线的对称轴对称,点B的坐标是(1,3),
∴点C的坐标是(3,3),
∴BC=3-1=2,BC∥x轴,
∴![]() 中,BC上的高为3,
中,BC上的高为3,
∴![]() 的面积=2×3÷2=3;
的面积=2×3÷2=3;
(3)∵点![]() 为抛物线上一动点,且位于第四象限,如图1,
为抛物线上一动点,且位于第四象限,如图1,
∴设![]() ,作
,作![]() 于点
于点![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() (舍去),
(舍去),![]() ,
,
∴![]() .
.
(4)以点C,M,N为顶点的三角形为等腰直角三角形时,分五类情况讨论:
①以点M为直角顶点且M在x轴上方时,如图2,CM=MN,∠CMN=90°,
∵∠CBM=∠MHN=90°,
∴∠BCM+∠BMC=90°,
∵∠HMN+∠BMC=90°,
∴∠BCM=∠HMN,
∴CBMMHN,
∴BC=MH=2,BM=HN=3-2=1,
∴N(2,0);
②以点M为直角顶点且M在x轴下方时,如图3,
作辅助线,构造如图所示的两直角三角形:RtNEM和RtMDC,同①的证法,
可得:RtNEMRtMDC,
∴EM=CD=5,
∵OH=1,
∴ON=NH-OH=5-1=4,
∴N(-4,0);
③以点N为直角顶点且N在y轴左侧时,如图4,CN=MN,∠MNC=90°,
作辅助线,构造如图所示的两直角三角形:RtNEM和Rt CDN,同理可得:
RtNEM Rt CDN,
∴ME=NH=DN=3,
∴ON=3-1=2,
∴N(-2,0);
④以点N为直角顶点且N在y轴右侧时,如图5,CN=MN,∠MNC=90°,
作辅助线,构造如图所示的两直角三角形:RtNEM和Rt CDN,同理可得:
RtNEMRtCDN,
∴ME=DN=NH=3
∴ON=1+3=4,
∴N(4,0);
⑤以C为直角顶点时,不能构成满足条件的等腰直角三角形;
综上所述:点N的坐标为:![]() ,
,![]() ,
,![]() ,
,![]() .
.
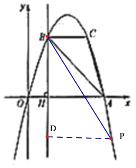
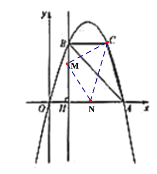
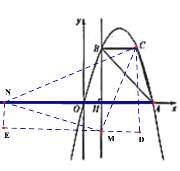
图1 图2 图3
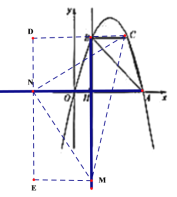
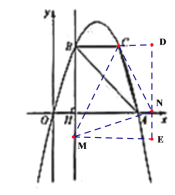
图4 图5


科目:初中数学 来源: 题型:
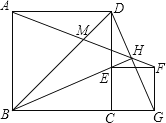
【题目】如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HEHB=4-2![]() ,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=
,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45°;③GD=![]() AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是______(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的![]() 的网格中,给出了以格点(网格线的交点)为端点的线段AB.
的网格中,给出了以格点(网格线的交点)为端点的线段AB.
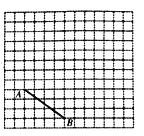
(1)将线段AB向上平移5个单位长度,得到线段![]() ,画出线段
,画出线段![]() ;连接
;连接![]() 、
、![]() ,并直接判断四边形
,并直接判断四边形![]() 的形状;
的形状;
(2)以点B为旋转中心,将线段AB顺时针旋转![]() 得到线段BC,画出线段BC,并直接写出
得到线段BC,画出线段BC,并直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某礼品店生产的礼品盒分为六个档次,第一档(最低档次)的产品每天生产76件,每件利润10元,调查表明:生产提高一个档次的礼品盒,每件利润增加2元.
(1)若生产的某批礼品盒每件利润为14元,问生产的是第几档次的产品?
(2)由于生产工序不同,礼品盒每提升一个档次,一天会少生产4件,若生产的某档次产品一天的利润为1080元,问生产的是第几档次的产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AE∥CD,CE∥AB.
(1)试判断四边形ADCE的形状,并证明你的结论.
(2)连接BE,若∠BAC=30°,CE=1,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
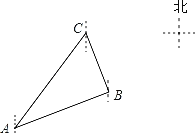
【题目】在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
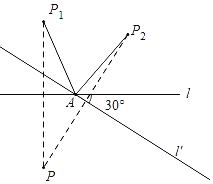
【题目】如图,点P是直线l外一个定点,点A为直线l上一个定点,点P关于直线l的对称点记为P1,将直线l绕点A顺时针旋转30°得到直线l′,此时点P2与点P关于直线l′对称,则∠P1AP2等于( )
A.30°B.45°C.60°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
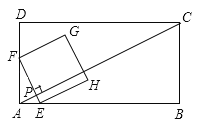
【题目】如图,在矩形![]() 中,
中,![]() .动点
.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒4个单位长度的速度向终点
以每秒4个单位长度的速度向终点![]() 运动.过点
运动.过点![]() (不与点
(不与点![]() 、
、![]() 重合)作
重合)作![]() ,交
,交![]() 或
或![]() 于点
于点![]() ,交
,交![]() 或
或![]() 于点
于点![]() ,以
,以![]() 为边向右作正方形
为边向右作正方形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)①![]() _________________;
_________________;
②当点![]() 在
在![]() 上时,用含
上时,用含![]() 的代数式直接表示线段
的代数式直接表示线段![]() 的长.
的长.
(2)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(3)设正方形![]() 的周长为
的周长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)直接写出对角线![]() 所在的直线将正方形
所在的直线将正方形![]() 分成两部分图形的面积比为1:2时
分成两部分图形的面积比为1:2时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com