练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如果一个四边形的对角线相等，那么顺次连接这个四边形各边中点所得的四边形一定是（ ）??
    A．梯形
    B．矩形
    C．菱形
    D．正方形
    【答案】分析：作出图形，根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=AC，GH=AC，HE=BD，FG=BD，再根据四边形的对角线相等可可知AC=BD，从而得到EF=FG=GH=HE，再根据四条边都相等的四边形是菱形即可得解．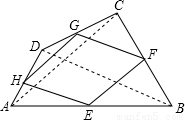
    解答：解：如图，E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点，
    根据三角形的中位线定理，EF=AC，GH=AC，HE=BD，FG=BD，
    连接AC、BD，
    ∵四边形ABCD的对角线相等，
    ∴AC=BD，
    所以，EF=FG=GH=HE，
    所以，四边形EFGH是菱形．
    故选C．
    点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，四条边都相等的四边形是菱形，熟记定理与判定方法是解题的关键，作出图形更形象直观．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    18、下列说法中不正确的是（　　）
    （1）如果一个四边形任意相邻的两个内角都互补，那么这个四边形是平行四边形；
    （2）一组对边平行，另一组对边相等的四边形是平行四边形；
    （3）如果AC，BD是四边形ABCD的对角线，且AC平分BD，那么，四边形ABCD是平行四边形；
    （4）两组对角分别相等的四边形是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

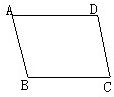    6、如图给出下列论断：①AD∥BC：②AB∥CD；③∠A=∠C．
    以上其中两个作为题设，另一个作为结论，用“如果…，那么…”形式，写出一个你认为正确的命题是
    如果一个四边形的两组对边平行，那么它的对角相等；或如果一个四边形的一组对边平行，一组对角相等，那么它的另一组对边也互相平行．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

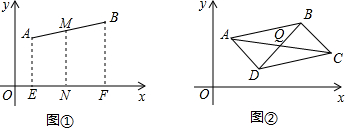    让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系．
    第一步：数轴上两点连线的中点表示的数．自己画一个数轴，如果点A、B分别表示-2、4，则线段AB的中点M表示的数是
    1
    1
    ． 再试几个，我们发现：数轴上连接两点的线段的中点所表示的数是这两点所表示数的平均数．
    第二步；平面直角坐标系中两点连线的中点的坐标（如图①）为便于探索，我们在第一象限内取两点A（x1，y1），B（x2，y2），取线段AB的中点M，分别作A、B到x轴的垂线段AE、BF，取EF的中点N，则MN是梯形AEFB的中位线，故MN⊥x轴，利用第一步的结论及梯形中位线的性质，我们可以得到点M的坐标是（
    x1+x2
    2
    x1+x2
    2
    ，
    y1+y2
    2
    y1+y2
    2
     ）（用x1，y1，x2，y2表示），AEFB是矩形时也可以．我们的结论是：平面直角坐标系中连接两点的线段的中点的横（纵）坐标等于这两点的横（纵）坐标的平均数．
    第三步：平面直角坐标系中平行四边形的顶点坐标之间的关系（如图②）在平面直角坐标系中画一个平行四边形ABCD，设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），则其对角线交点Q的坐标可以表示为Q（
    x1+x3
    2
    x1+x3
    2
    ，
    y1+y3
    2
    y1+y3
    2
    ），也可以表示为Q（
    x2+x4
    2
    x2+x4
    2
    ，
    y2+y4
    2
    y2+y4
    2
     ），经过比较，我们可以分别得出关于x1，x2，x3，x4及，y1，y2，y3，y4的两个等式是
    x1+x3=x2+x4
    x1+x3=x2+x4
    和
    y1+y3=y2+y4
    y1+y3=y2+y4
    ． 我们的结论是：平面直角坐标系中平行四边形的对角顶点的横（纵）坐标的
    和相等
    和相等
    ．

    查看答案和解析>>

    科目：初中数学 来源：101网校同步练习　初二数学　华东师大(新课标2001－3年初审) 华东师大(新课标2001－3年初审) 题型：022

    如果一个四边形的对角线相等，且对角线平分每组对角，那么该四边形是________形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：022

    如果一个四边形的对角线相等，且对角线平分每组对角，那么该四边形是　　　　 　　　　形

    查看答案和解析>>

    同步练习册答案