
 已知抛物线y=$\frac{1}{2}$x2-x-4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点C作直线1∥x轴.将该抛物线在y轴左侧的部分沿直线1翻折,抛物线的其余部分保持不变.得到一个新的图象,记为G.请你结合图象问答:当直线y=$\frac{1}{2}$x+b与图象G只有一个公共点时,求b的取值范围.
已知抛物线y=$\frac{1}{2}$x2-x-4与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点C作直线1∥x轴.将该抛物线在y轴左侧的部分沿直线1翻折,抛物线的其余部分保持不变.得到一个新的图象,记为G.请你结合图象问答:当直线y=$\frac{1}{2}$x+b与图象G只有一个公共点时,求b的取值范围. 分析 分别令x=0、y=0,得到方程,解方程即可求得A、B.C点的坐标,然后分两种情况分别讨论即可得出b的取值范围.
解答  解:令y=0,
解:令y=0,
∴$\frac{1}{2}$-x-4=0,解得x=-2或x=4,
∴A(-2,0),B(4,0),
令x=0,则y=-4,
∴C(0,-4),
①当直线过C(0,-4)时,b=-4,
∴b>-4;
②当直线与抛物线只有应该交点时,∴$\frac{1}{2}$-x-4=$\frac{1}{2}$x+b,
整理得,x2-3x-8-2b=0,
∵△=9+4(8+2b)=0,
∴b=-$\frac{41}{8}$,
∴b<-$\frac{41}{8}$,
综上,结合图象可知,b的取值范围为b>-4或b<-$\frac{41}{8}$.
点评 本题考查了二次函数的图象与结合变换,抛物线与坐标轴的交点,主要考查学生数形结合的数学思想方法.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:选择题
| A. | 10000 m | B. | 1000 m | C. | 100 m | D. | 10 m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
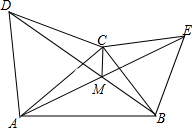 如图,已知在△ABC中,分别以AC、BC为边向外作正△BCE,正△ACD,BD与AE交于M.
如图,已知在△ABC中,分别以AC、BC为边向外作正△BCE,正△ACD,BD与AE交于M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,∠BAC=45°,AE是∠BAC的平分线,CD⊥AB于D,交AE于点F.请探索AF与BC之间的数量关系,并说明理由.
如图,在△ABC中,AB=AC,∠BAC=45°,AE是∠BAC的平分线,CD⊥AB于D,交AE于点F.请探索AF与BC之间的数量关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
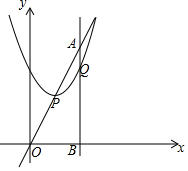 如图,点A(2,4),作AB⊥x铀于点B,抛物线y=x2+bx+c的顶点P在直线OA上,且抛物线交线段AB于点Q,求线段AQ的最大值及此时抛物线的解析式.
如图,点A(2,4),作AB⊥x铀于点B,抛物线y=x2+bx+c的顶点P在直线OA上,且抛物线交线段AB于点Q,求线段AQ的最大值及此时抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
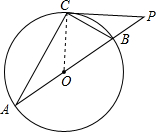 如图,AB是圆O直径,C是圆O上一点,P在AB延长线上,且∠PCB=∠A.
如图,AB是圆O直径,C是圆O上一点,P在AB延长线上,且∠PCB=∠A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com