
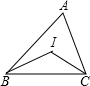
 实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数,
实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数, ∠ABC+
∠ABC+ ∠ACB=
∠ACB= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A),在△IBC中,利用三角形内角和定理求∠BIC.
(180°-∠A),在△IBC中,利用三角形内角和定理求∠BIC. (∠ABC+∠ACB)=40°,
(∠ABC+∠ACB)=40°, (∠ABC+∠ACB)=30°,
(∠ABC+∠ACB)=30°, ∠A
∠A ∠ABC,∠ICB=
∠ABC,∠ICB= ∠ACB
∠ACB ∠ABC+
∠ABC+ ∠ACB=
∠ACB= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A)
(180°-∠A) (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A
∠A ∠A.
∠A.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
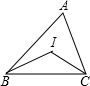 实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数,
实践与探索!如图,△ABC中,∠ABC与∠ACB的平分线交于点I,根据下列条件,求∠BIC的度数,查看答案和解析>>
科目:初中数学 来源: 题型:
 实践与探索:
实践与探索:查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏扬州江都麾村中学八年级第一次月考数学试题(解析版) 题型:解答题
实践与探索:
㈠小明在玩积木游戏时,把三个正方形积木摆成一定的形状,正视图如图①,
问题(1):若此中的三角形△DEF为直角三角形,P的面积为9,Q的面积为15,则M的面积为_______。

问题(2):若P的面积为36cm2,Q的面积为64 cm2,同时M的面积为100 cm2,则△DEF为_______三角形。
㈡图形变化:Ⅰ.如图②,分别以直角三角形的三边为直径向三角形外作三个半圆,你能找出这三个半圆的面积之间有什么关系吗?请说明理由。
Ⅱ.如图③,如果直角三角形两直角边的长分别为3和4,以直角三角形的三边为直径作半圆,你能利用上面中的结论求出阴影部分的面积吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com