
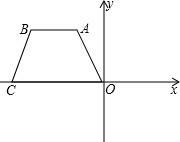
 为2
为2 ,AB=4.
,AB=4.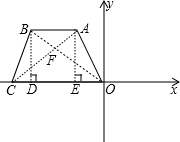 解:(1)过A作AE⊥OC于E,过B作BD⊥OC于D,如图,
解:(1)过A作AE⊥OC于E,过B作BD⊥OC于D,如图, ,即AE=2
,即AE=2 ,
, AE=
AE= ×2
×2 =2,
=2, (4+8)×2
(4+8)×2 =12
=12 ;
; ),B点坐标为(-6,2
),B点坐标为(-6,2 ),C点坐标为(-8,0),
),C点坐标为(-8,0), )代入得k=-
)代入得k=- ,即直线OB的解析式为y=-
,即直线OB的解析式为y=- x①;
x①; )和C(-8,0)代入得k=
)和C(-8,0)代入得k= ,b=
,b= ,即直线AC的解析式为y=
,即直线AC的解析式为y= x+
x+ ②;
②; ,
, ),
), ,
, )代入得k=-
)代入得k=-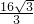 ,
,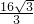 x.
x. ,在Rt△OAE中,根据含30度的直角三角形三边的关系得到OE,利用等腰梯形的性质得到CD,然后根据梯形的面积公式计算即可;
,在Rt△OAE中,根据含30度的直角三角形三边的关系得到OE,利用等腰梯形的性质得到CD,然后根据梯形的面积公式计算即可; ),B点坐标为(-6,2
),B点坐标为(-6,2 ),C点坐标为(-8,0),然后利用待定系数法确定直线OB和AC的解析式,在通过建立方程组求出它们交点的坐标,然后再利用待定系数法求出反比例函数的解析式.
),C点坐标为(-8,0),然后利用待定系数法确定直线OB和AC的解析式,在通过建立方程组求出它们交点的坐标,然后再利用待定系数法求出反比例函数的解析式.

科目:初中数学 来源: 题型:
| 4 | 3 |
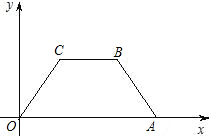 一腰平行的直线将该梯形分成面积相等的两部分?若存在,请求出点P的横坐标;若不存在,请说明理由.
一腰平行的直线将该梯形分成面积相等的两部分?若存在,请求出点P的横坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
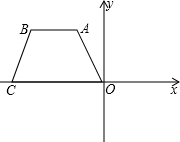 为2
为2| 3 |
查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》中考题集(32):27.3 实践与探索(解析版) 题型:解答题
 ,点B的坐标为(7,4).
,点B的坐标为(7,4).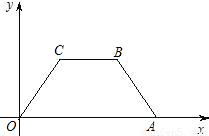
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(30):2.4 二次函数的应用(解析版) 题型:解答题
 ,点B的坐标为(7,4).
,点B的坐标为(7,4).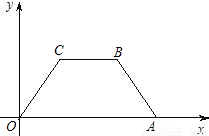
查看答案和解析>>
科目:初中数学 来源:第23章《二次函数与反比例函数》中考题集(30):23.5 二次函数的应用(解析版) 题型:解答题
 ,点B的坐标为(7,4).
,点B的坐标为(7,4).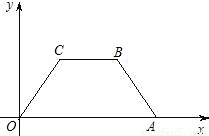
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com