
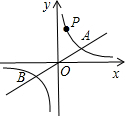
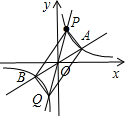
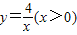 的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,设点P的坐标为(x,y).
的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,设点P的坐标为(x,y).
 解:(1)设点P的坐标为(x,y),
解:(1)设点P的坐标为(x,y),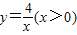 的一个分支上的一点,
的一个分支上的一点,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
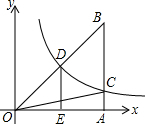 (2013•福田区一模)如图,已知双曲线y=
(2013•福田区一模)如图,已知双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
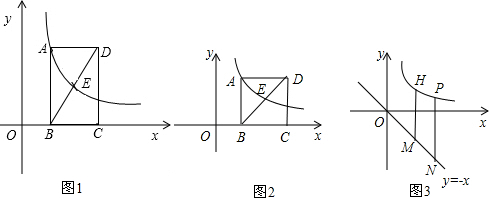
| k |
| x |
| k1 |
| x |
| 2 |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 锡尚德公司和中国船舶重工集团第702研究所.图一是游船的某一部件的设计图纸.(其中∠A、∠B、∠C是直角,DE是双曲线的一部分,AE的长为30cm,AB的长为40cm,BC的长为60cm)
锡尚德公司和中国船舶重工集团第702研究所.图一是游船的某一部件的设计图纸.(其中∠A、∠B、∠C是直角,DE是双曲线的一部分,AE的长为30cm,AB的长为40cm,BC的长为60cm)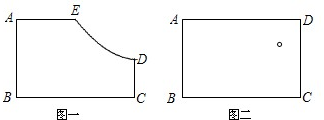
查看答案和解析>>
科目:初中数学 来源: 题型:
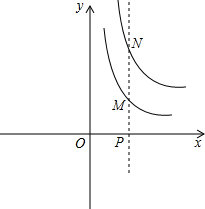 【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段)
【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段)| 2 |
| x |
| 3 |
| x |
| MN |
| PM |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com