
分析 先根据十字相乘法确定m,n的值,再代入代数式,即可解答.
解答 解:∵x2+mx-15=(x+3)(x+n),
∴x2+mx-15=x2+nx+3x+3n,
∴x2+mx-15=x2+(n+3)x+3n.
∴$\left\{\begin{array}{l}{m=n+3}\\{3n=-15}\end{array}\right.$
∴$\left\{\begin{array}{l}{m=-2}\\{n=-5}\end{array}\right.$
∴3m2+4n-1=3×(-2)2+4×(-5)-1=3×4-20-1=12-20-1=-9.
故答案为:-9.
点评 本题考查了因式分解,解决本题的关键是根据十字相乘法确定m,n的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.5π cm2 | B. | 30π cm2 | C. | 15π cm2 | D. | 22.5π cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
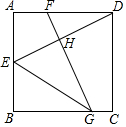 已知:如图,正方形ABCD中,E是AB上一点,FG⊥DE于点H.
已知:如图,正方形ABCD中,E是AB上一点,FG⊥DE于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
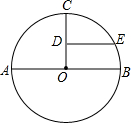 在⊙O中,AB是直径,CO⊥AB,D是CO的中点,DE∥AB,则$\widehat{CE}$与$\widehat{BE}$之间的等量关系是什么?请证明你的结论.
在⊙O中,AB是直径,CO⊥AB,D是CO的中点,DE∥AB,则$\widehat{CE}$与$\widehat{BE}$之间的等量关系是什么?请证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com