
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒. 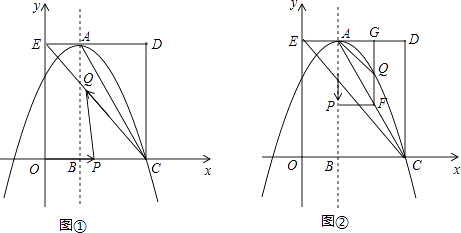
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
【答案】
(1)解:(1,4);y=﹣x2+2x+3
(2)解:依题意有:OC=3,OE=4,
∴CE= ![]() =
= ![]() =5,
=5,
当∠QPC=90°时,
∵cos∠QCP= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() ;
;
当∠PQC=90°时,
∵cos∠QCP= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() .
.
∴当t= ![]() 或t=
或t= ![]() 时,△PCQ为直角三角形
时,△PCQ为直角三角形
(3)解:∵A(1,4),C(3,0),
设直线AC的解析式为y=kx+b,则
![]() ,
,
解得 ![]() .
.
故直线AC的解析式为y=﹣2x+6.
∵P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得x=1+ ![]() ,
,
∴Q点的横坐标为1+ ![]() ,
,
将x=1+ ![]() 代入y=﹣(x﹣1)2+4中,得y=4﹣
代入y=﹣(x﹣1)2+4中,得y=4﹣ ![]() .
.
∴Q点的纵坐标为4﹣ ![]() ,
,
∴QF=(4﹣ ![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣ ![]() ,
,
∴S△ACQ=S△AFQ+S△CFQ
= ![]() FQAG+
FQAG+ ![]() FQDG
FQDG
= ![]() FQ(AG+DG)
FQ(AG+DG)
= ![]() FQAD
FQAD
= ![]() ×2(t﹣
×2(t﹣ ![]() )
)
=﹣ ![]() +t
+t
=﹣ ![]() (t2+4﹣4t﹣4)
(t2+4﹣4t﹣4)
=﹣ ![]() (t﹣2)2+1,
(t﹣2)2+1,
∴当t=2时,△ACQ的面积最大,最大值是1
【解析】解:(1)∵抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上, ∴点A坐标为(1,4),
设抛物线的解析式为y=a(x﹣1)2+4,
把C(3,0)代入抛物线的解析式,可得a(3﹣1)2+4=0,
解得a=﹣1.
故抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(1)根据抛物线的对称轴与矩形的性质可得点A坐标,根据待定系数法可得抛物线的解析式;(2)先根据勾股定理可得CE,再分两种情况:当∠QPC=90°时;当∠PQC=90°时;讨论可得△PCQ为直角三角形时t的值;(3)根据待定系数法可得直线AC的解析式,根据S△ACQ=S△AFQ+S△CPQ可得S△ACQ=﹣ ![]() (t﹣2)2+1,依此即可求解.
(t﹣2)2+1,依此即可求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
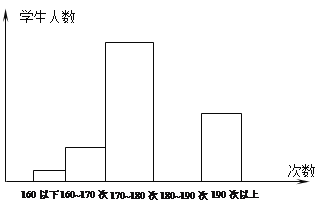
【题目】为了解中学生的体能情况,某校抽取了50名八年级学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频数分布直方图如下图所示已知图中从左到右前第一、第二、第三、第五小组的频率分别为0.04 , 0.12 ,0.4 ,O.28 ,根据已知条件解答下列问题:
(1)第四个小组的频率是多少? 你是怎样得到的?
(2)这五小组的频数各是多少?
(3)在这次跳绳中,跳绳次数的中位数落在第几小组内?
(4)将频数分布直方图补全,并分别写出各个小组的频数,并画出频数分布折线图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入![]() 表是某周的生产情况
表是某周的生产情况![]() 超产为正、减产为负
超产为正、减产为负![]() :
:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产多少辆;
根据记录可知前三天共生产多少辆;
![]() 产量最多的一天比产量最少的一天多生产多少辆;
产量最多的一天比产量最少的一天多生产多少辆;
![]() 该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④ ![]() 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两站相距240千米,从甲站开出一列慢车,速度为每小时80千米,从乙站开出一列快车,速度为每小时120千米.
(1)若两车同时开出,背向而行,则经过多长时间两车相距540千米?
(2)若两车同时开出,同向而行(快车在后),则经过多长时间快车可追上慢车?
(3)若两车同时开出,同向而行(慢车在后),则经过多长时间两车相距300千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22-12,16=52-32,则3和16是智慧数).已知按从小到大的顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…则第2 013个“智慧数”是______.
【答案】2 687
【解析】解析:观察数的变化规律,可知全部“智慧数”从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数,归纳可得,第n组的第一个数为4n(n≥2).因为2 013÷3=671,所以第2 013个“智慧数”是第671组中的第3个数,即为4×671+3=2 687.
点睛:找规律题需要记忆常见数列
1,2,3,4……n
1,3,5,7……2n-1
2,4,6,8……2n
2,4,8,16,32……![]()
1,4,9,16,25……![]()
2,6,12,20……n(n+1)
一般题目中的数列是利用常见数列变形而来,其中后一项比前一项多一个常数,是等差数列,列举找规律.后一项是前一项的固定倍数,则是等比数列,列举找规律.
【题型】填空题
【结束】
19
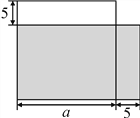
【题目】如图,郑某把一块边长为a m的正方形的土地租给李某种植,他对李某说:“我把你这块地的一边减少5 m,另一边增加5 m,继续租给你,你也没有吃亏,你看如何”.李某一听,觉得自己好像没有吃亏,就答应了.同学们,你们觉得李某有没有吃亏?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)992-102×98;
(2)[x(x2y2-xy)-y(x2-x3y)]÷x2y.
【答案】(1)-195(2)2xy-2
【解析】试题分析:(1)利用平方差公式,完全平方公式简便计算.
(2)提取公因式,化简.
试题解析:
(1)原式=(100-1)2-(100+2)×(100-2)
=(1002-200+1)-(1002-4)=-200+5=-195.
(2)原式=[x2y(xy-1)-x2y(1-xy)]÷x2y
=2x2y(xy-1)÷x2y=2(xy-1)=2xy-2.
【题型】解答题
【结束】
21
【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,E 是直线 CD 上的一点,且 ∠BAE=30°, 是直线 CD 上的一动点,M是 AP 的中点,直线 MN⊥AP 且与 CD 交于点 N,设 ∠BAP=X°,∠MNE=Y°.

(1)在图2 中,当 x=12 时,∠MNE= ;在图 3 中,当 x=50 时,∠MNE= ;
(2)研究表明:y与x之间关系的图象如图4所示( 不存在时,用空心点表示),请你根据图象直接估计当 y=100 时,x= ;

(3)探究:当 x= 时,点 N 与点 E 重合;
(4)探究:当 x>105 时,求y与x之间的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com