
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=x2+![]() гыyжсЯрНЛгкЕуAЃЌЕуBгыЕуOЙигкЕуAЖдГЦ
гыyжсЯрНЛгкЕуAЃЌЕуBгыЕуOЙигкЕуAЖдГЦ
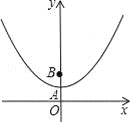
ЃЈ1ЃЉЬюПеЃКЕуBЕФзјБъЪЧ ЃЛ
ЃЈ2ЃЉЙ§ЕуBЕФжБЯпy=kx+bЃЈЦфжаkЃМ0ЃЉгыxжсЯрНЛгкЕуCЃЌЙ§ЕуCзїжБЯпlЦНаагкyжсЃЌPЪЧжБЯпlЩЯвЛЕуЃЌЧвPB=PCЃЌЧѓЯпЖЮPBЕФГЄЃЈгУКЌkЕФЪНзгБэЪОЃЉЃЌВЂХаЖЯЕуPЪЧЗёдкХзЮяЯпЩЯЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєЕуCЙигкжБЯпBPЕФЖдГЦЕуCЁфЧЁКУТфдкИУХзЮяЯпЕФЖдГЦжсЩЯЃЌЧѓДЫЪБЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ0ЃЌ![]() ЃЉЃЛЃЈ2ЃЉЕуPдкХзЮяЯпЩЯ,РэгЩЯъМћНтЮіЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ
ЃЉЃЛЃЈ2ЃЉЕуPдкХзЮяЯпЩЯ,РэгЩЯъМћНтЮіЃЛЃЈ3ЃЉPЕузјБъЮЊЃЈ![]() ЃЌ1ЃЉЃЎ
ЃЌ1ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩХзЮяЯпНтЮіЪНПЩЧѓЕУЕуAЕФзјБъЃЌдйРћгУЖдГЦПЩЧѓЕУBЕузјБъЃЛЃЈ2ЃЉПЩЯШгУkБэЪОГіCЕузјБъЃЌЙ§BзїBDЁЭlгкЕуDЃЌЬѕМўПЩжЊPЕудкxжсЩЯЗНЃЌЩшPЕузнзјБъЮЊyЃЌПЩБэЪОГіPDЁЂPBЕФГЄЃЌдкRtЁїPBDжаЃЌРћгУЙДЙЩЖЈРэПЩЧѓЕУyЃЌдђПЩЧѓГіPBЕФГЄЃЌДЫЪБПЩЕУГіPЕузјБъЃЌДњШыХзЮяЯпНтЮіЪНПЩХаЖЯPЕудкХзЮяЯпЩЯЃЛЃЈ3ЃЉРћгУЦНааЯпКЭжсЖдГЦЕФаджЪПЩЕУЕНЁЯOBC=ЁЯCBP=ЁЯCЁфBP=60ЁуЃЌдђПЩЧѓЕУOCЕФГЄЃЌДњШыХзЮяЯпНтЮіЪНПЩЧѓЕУPЕузјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпХзЮяЯпy=x2+![]() гыyжсЯрНЛгкЕуAЃЌ
гыyжсЯрНЛгкЕуAЃЌ
ЁрAЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЕуBгыЕуOЙигкЕуAЖдГЦЃЌ
ЁрBA=OA=![]() ЃЌ
ЃЌ
ЁрOB=![]() ЃЌМДBЕузјБъЮЊЃЈ0ЃЌ
ЃЌМДBЕузјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЙЪД№АИЮЊЃКЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉЁпBЕузјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁржБЯпНтЮіЪНЮЊy=kx+![]() ЃЌСюy=0ПЩЕУkx+
ЃЌСюy=0ПЩЕУkx+![]() =0ЃЌНтЕУx=Љ
=0ЃЌНтЕУx=Љ![]() ЃЌ
ЃЌ
ЁрOC=Љ![]() ЃЌ
ЃЌ
ЁпPB=PCЃЌ
ЁрЕуPжЛФмдкxжсЩЯЗНЃЌ
ШчЭМ1ЃЌЙ§BзїBDЁЭlгкЕуDЃЌЩшPB=PC=mЃЌ
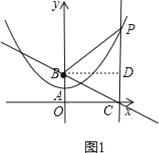
дђBD=OC=Љ![]() ЃЌCD=OB=
ЃЌCD=OB=![]() ЃЌ
ЃЌ
ЁрPD=PCЉCD=mЉ![]() ЃЌ
ЃЌ
дкRtЁїPBDжаЃЌгЩЙДЙЩЖЈРэПЩЕУPB2=PD2+BD2ЃЌ
МДm2=ЃЈmЉ![]() ЃЉ2+ЃЈЉ
ЃЉ2+ЃЈЉ![]() ЃЉ2ЃЌНтЕУm=
ЃЉ2ЃЌНтЕУm=![]() +
+![]() ЃЌ
ЃЌ
ЁрPB=![]() +
+![]() ЃЌ
ЃЌ
ЁрPЕузјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() +
+![]() ЃЉЃЌ
ЃЉЃЌ
ЕБx=Љ![]() ЪБЃЌДњШыХзЮяЯпНтЮіЪНПЩЕУy=
ЪБЃЌДњШыХзЮяЯпНтЮіЪНПЩЕУy=![]() +
+![]() ЃЌ
ЃЌ
ЁрЕуPдкХзЮяЯпЩЯЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгCCЁфЃЌ
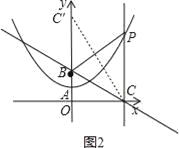
ЁпlЁЮyжсЃЌ
ЁрЁЯOBC=ЁЯPCBЃЌ
гжPB=PCЃЌ
ЁрЁЯPCB=ЁЯPBCЃЌ
ЁрЁЯPBC=ЁЯOBCЃЌ
гжCЁЂCЁфЙигкBPЖдГЦЃЌЧвCЁфдкХзЮяЯпЕФЖдГЦжсЩЯЃЌМДдкyжсЩЯЃЌ
ЁрЁЯPBC=ЁЯPBCЁфЃЌ
ЁрЁЯOBC=ЁЯCBP=ЁЯCЁфBP=60ЁуЃЌ
дкRtЁїOBCжаЃЌOB=![]() ЃЌдђBC=1
ЃЌдђBC=1
ЁрOC=![]() ЃЌМДPЕуЕФКсзјБъЮЊ
ЃЌМДPЕуЕФКсзјБъЮЊ![]() ЃЌДњШыХзЮяЯпНтЮіЪНПЩЕУy=ЃЈ
ЃЌДњШыХзЮяЯпНтЮіЪНПЩЕУy=ЃЈ![]() ЃЉ2+
ЃЉ2+![]() =1ЃЌ
=1ЃЌ
ЁрPЕузјБъЮЊЃЈ![]() ЃЌ1ЃЉЃЎ
ЃЌ1ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=12ЃЌBC=5ЃЌНЋЁїABCШЦБпACЫљдкжБЯпа§зЊвЛжмЕУЕНдВзЖЃЌдђИУдВзЖЕФВрУцЛ§ЪЧ( )
A. 25Іа B. 65Іа C. 90Іа D. 130Іа
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЦНУцжБНЧзјБъЯЕжаЃЌКЏЪ§y=ax+bгыy=ax2ЉbxЕФЭМЯѓПЩФмЪЧЃЈ ЃЉ
AЃЎ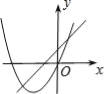 BЃЎ
BЃЎ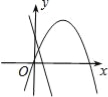 CЃЎ
CЃЎ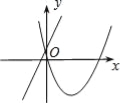 DЃЎ
DЃЎ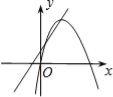
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИажЊЃКШчЭМ1ЃЌADЦНЗжЁЯBACЃЎЁЯB+ЁЯC=180ЁуЃЌЁЯB=90ЁуЃЌвзжЊЃКDB=DCЃЎ
ЬНОПЃКШчЭМ2ЃЌADЦНЗжЁЯBACЃЌЁЯABD+ЁЯACD=180ЁуЃЌЁЯABDЃМ90ЁуЃЌЧѓжЄЃКDB=DCЃЎ
гІгУЃКШчЭМ3ЃЌЫФБпаЮABCDжаЃЌЁЯB=45ЁуЃЌЁЯC=135ЁуЃЌDB=DC=aЃЌдђABЉAC= ЃЈгУКЌaЕФДњЪ§ЪНБэЪОЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШ§ИіСЌајЕФе§ЦцЪ§ЃЌзюДѓЪ§гызюаЁЪ§ЕФЛ§БШжаМфвЛИіЪ§ЕФ6БЖЖр3ЃЌЧѓетШ§ИіЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯпmЭтгавЛЖЈЕуAЃЌAЕНжБЯпmЕФОрРыЪЧ7 cmЃЌBЪЧжБЯпmЩЯЕФШЮвтвЛЕуЃЌдђЯпЖЮABЕФГЄЖШЃКAB___________7 cm.(ЬюаДЁАЃМЁБЁАЃОЁБЁАЃНЁБЁАЁмЁБЛђЁАЁнЁБ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗНГЬx2Ѓ4xЃН0жаЃЌb2Ѓ4acЕФжЕЮЊ( )
A. Ѓ16 B. 16 C. 4 D. Ѓ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаФГжабЇОіЖЈдкбЇЩњжаПЊеЙЖЊЩГАќЁЂДђРКЧђЁЂЬјДѓЩўКЭЬпыІЧђЫФжжЯюФПЕФЛюЖЏЃЌЮЊСЫНтбЇЩњЖдЫФжжЯюФПЕФЯВЛЖЧщПіЃЌЫцЛњЕїВщСЫИУаЃmУћбЇЩњзюЯВЛЖЕФвЛжжЯюФПЃЈУПУћбЇЩњБибЁЧвжЛФмбЁдёЫФжжЛюЖЏЯюФПЕФвЛжжЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТЕФВЛЭъећЕФЭГМЦЭМБэЃК
бЇЩњзюЯВЛЖЕФЛюЖЏЯюФПЕФШЫЪ§ЭГМЦБэ
ЯюФП | бЇЩњЪ§ЃЈУћЃЉ | АйЗжБШ |
ЖЊЩГАќ | 20 | 10% |
ДђРКЧђ | 60 | p% |
ЬјДѓЩў | n | 40% |
ЬпыІЧђ | 40 | 20% |
ИљОнЭМБэжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉm= ЃЌn= ЃЌp= ЃЛ
ЃЈ2ЃЉЧыИљОнвдЩЯаХЯЂжБНгВЙШЋЬѕаЮЭГМЦЭМЃЛ

ЃЈ3ЃЉИљОнГщбљЕїВщНсЙћЃЌЧыФуЙРМЦИУаЃ2000УћбЇЩњжагаЖрЩйУћбЇЩњзюЯВЛЖЬјДѓЩўЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШ§НЧаЮЕФСНБпГЄЗжБ№ЮЊ8КЭ4ЃЌдђЕкШ§БпГЄПЩФмЪЧЃЈ ЃЉ
A.3
B.4
C.8
D.12
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com