练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

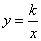    在平面直角坐标系xOy中，一次函数的图象与反比例函数的图象的一

    个交点为A（1，）.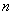

    （1）求反比例函数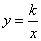的解析式；

    （2）若P是坐标轴上一点（P不与O重合），且满足，直接写出点P的坐标.


     ⑴ ∵点A(1,n)在一次函数的图象上，

    ∴n=3．

    ∴点A的坐标为(1,3)．

    ∵点的反比例函数的图象上，

    ∴k=3．

    ∴反比例函数的解析式为．

     ⑵ 点P的坐标为(2,0)或(0,6)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，在中，，以为直径作⊙，交于点，连接，过点作⊙的

    切线，交延长线于点，交于点。

    （1）求证：；

    （2）当，时，求及的长。

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：如图，点A、B、C在同一直线上，AD∥CE，AD=AC，∠D=∠CAE.

    求证：DB=AE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列图形中，是中心对称图形但不是轴对称图形的是

    A．等边三角形                  B．菱形       

    C. 平行四边形                   D．矩形

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，正三角形ABC、正四边形ABCM、正五边形ABCMN中，点E在CB的延长线

    上，点D在另一边反向延长线上，且BE=CD，DB延长线交AE于点F．

    图1中∠AFB的度数为      ，图2中∠AFB度数为      ， 若将条件“正三角形、

    正四边形、正五边形”改为“正n边形”，其它条件不变，则∠AFB度数为         ．

    （用含n的代数式表示）

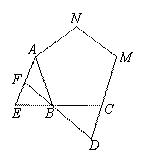
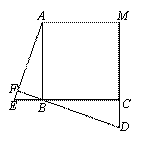
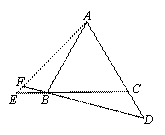
              图1                        图2                     图3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    阅读下面资料：
    小明遇到这样一个问题：如图1，对面积为a的△ABC逐次进行以下操作：分别延长AB、

    BC、CA至A1、B1、C1，使得A1B=AB，B1C=BC，C1A=CA，顺次连接A1、B1、C1，

    得到△A1B1C1，记其面积为S1，求S1的值．
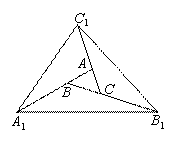
    小明是这样思考和解决这个问题的：如图2，连接A1C、B1A、C1B，因为A1B=AB，

    B1C=BC，C1A=CA，根据等高两三角形的面积比等于底之比，

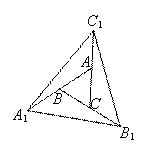
    图1 图2




    所以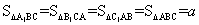，由此继续推理，从而解决了这个问题．


    （1）请直接写出S1= ；（用含字母a的式子表示）．
    请参考小明同学思考问题的方法，解决下列问题：
    （2）如图3，对面积为a的△ABC逐次进行以下操作：分别延长AB、BC、CA至A1、

    B1、C1，使得A1B=2AB，B1C=2BC，C1A=2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其

    面积为S2，求S2的值．

    （3）如图4，P为△ABC内一点，连接AP、BP、CP并延长分别交边BC、AC、AB于

    点D、E、F，则把△ABC分成六个小三角形，其中四个小三角形面积已在图上标明，设△APE的面积为y，△BPF的面积为x，

    ①求△APE ，△BPF，△APF 面积之间的关系；

    ②求△ABC的面积．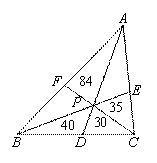


    图3

    图4




    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为了解居民用水情况，晓娜在某小区随机抽查了10户家庭的月用水量，结果如下表：

    月用水量（吨）

    5

    6

    7

    8

    9

    10

    户数

    1

    1

    2

    2

    3

    1

      

       则这10户家庭的月用水量的平均数和众数分别是

       A．7.8，9　　　 B．7.8，3　　    　C．4.5，9　　   D．4.5，3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，⊙是△的外接圆，，连结并延长交⊙的切线于点．

       （1）求证：；

    （2）若，，求的长．

     

     

     

     

     

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     “减去一个数，等于加上这个数的相反数”是实数的减法法则，请通过字母表示数，借助符号描述该法则：       ．

    查看答案和解析>>

    同步练习册答案