
分析 (1)根据方程有两个不相等的实数根,得到根的判别式的值大于0列出关于k的不等式,求出不等式的解集即可得到k的范围;
(2)找出k范围中的整数解确定出k的值,再将k的值代入原方程,求出方程的根,经检验即可得到满足题意的k的值.
解答 解:(1)△=(-6)2-4(k+3)=36-4k-12=-4k+24,
∵原方程有两个不相等的实数根,
∴-4k+24>0.
解得 k<6;
(2)∵k<6且k为大于3的整数,
∴k=4或5.
①当k=4时,方程x2-6x+7=0的根不是整数.
∴k=4不符合题意;
②当k=5时,方程x2-6x+8=0根为x1=2,x2=4均为整数.
∴k=5符合题意.
综上所述,k的值是5.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
也考查了一元二次方程的解法.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 地区类别 | 首小时内 | 首小时外 |
| 一类 | 2.5元/15分钟 | 3.75元/15分钟 |
| 二类 | 1.5元/15分钟 | 2.25元/15分钟 |
| 三类 | 0.5元/15分钟 | 0.75元/15分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
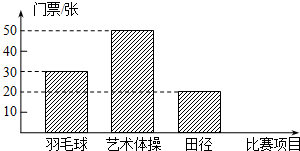 2010年5月20日上午10时起,2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分门票价格,如图为某公司购买的门票种类、数量所绘制成的条形统计图.
2010年5月20日上午10时起,2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分门票价格,如图为某公司购买的门票种类、数量所绘制成的条形统计图.| 比赛项目 | 票价(元/张) |
| 羽毛球 | 400 |
| 艺术体操 | 240 |
| 田径 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≥-1 | B. | m>-1 | C. | m≥-1且m≠0 | D. | m>-1且m≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
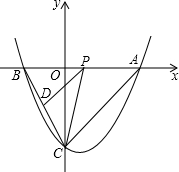 如图,抛物线y=$\frac{1}{2}{x^2}$-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.
如图,抛物线y=$\frac{1}{2}{x^2}$-x-4与坐标轴相交于A、B、C三点,P是线段AB上一动点(端点除外),过P作PD∥AC,交BC于点D,连接CP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 12 | C. | 16 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com