
分析 (1))①-②×2即可求出y,把y的值代入②即可求出x.
(2)先整理,再①+②得出6x=18,求出x=3,把x=3代入①求出y即可;
(3)首先去分母,然后去括号,再移项合并同类项,把x的系数化为1,即可得到不等式的解集.
(4)求出两个不等式的解集,根据找不等式组解集的规律找出即可.
解答 解:(1)$\left\{\begin{array}{l}{6x+11y=16①}\\{3x+5y=7②}\end{array}\right.$
∵①-②×2得:y=2,
把y=2代入②得:3x+10=7,
解得:x=-1,
∴方程组的解为:$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$;
(2)化简得:$\left\{\begin{array}{l}{3x-2y=8①}\\{3x+2y=10②}\end{array}\right.$
①+②得:6x=18,
解得:x=3,
把x=3代入①得:y=$\frac{1}{2}$,
∴方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=\frac{1}{2}}\end{array}\right.$;
(3)去分母得:4(x+1)<5(x-1)-6,
去括号得:4x+4<5x-5-6
移项得:4x-5x<-5-6-4,
合并同类项得:-x>-15,
把x的系数化为1得:x>15.
(4)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$
由①得:x≤1,
由②得:x>-2,
∴不等式组的解集为-2<x≤1,
在数轴上表示不等式组的解集为:
故整数解-1,0,1.
点评 本题考查了解二元一次方程组和解一元一次不等式组的整数解,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
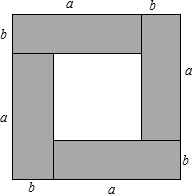 数学结合是一种重要的数学思想,借助这种方法我们可以将抽象的数学知识变得直观且具有可操作性,初中数学里的代数公式,有很多都可以通过表示几何图形面积的方法进行推导和验证,例如完全平方公式.下面我们进行类似的探究:
数学结合是一种重要的数学思想,借助这种方法我们可以将抽象的数学知识变得直观且具有可操作性,初中数学里的代数公式,有很多都可以通过表示几何图形面积的方法进行推导和验证,例如完全平方公式.下面我们进行类似的探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=kx+b与双曲线y=$\frac{m}{x}$交于点A(n,-2),B(2,1).
如图,直线y=kx+b与双曲线y=$\frac{m}{x}$交于点A(n,-2),B(2,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com