
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
(1)如图1,AE平分∠CAB交BC于E,交CD于F,若DF=2,求AC的长;
(2)将图1中的△ADC绕点D顺时针旋转一定角度得到△ADN,如图2,P,Q分别为线段AN,BC的中点,连接AC,BN,PQ,求证:BN=![]() PQ.
PQ.

【答案】(1)AC4+2![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)利用角平分线定理求出FM,再利用等腰直角三角形的性质即可得出CF,最后用![]() 即可;
即可;
(2)先判断出![]() ,再判断出∠PDQ=∠NDB,进而得出,△PDQ∽△NDB即可判断出结论;
,再判断出∠PDQ=∠NDB,进而得出,△PDQ∽△NDB即可判断出结论;
(1)如图1,
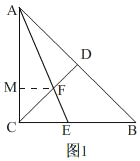
∵等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
∴CD⊥AB,∠ACD=45°
过点F作FM⊥AC,
∵AE平分∠CAB,
∴FM=FD=2
在Rt△CMF中,∠ACD=45°,
∴![]()
∴![]()
∵CD是等腰直角三角形斜边的中线,
∴![]()
(2)如图2,连接DP,DQ,

∵△ADC绕点D顺时针旋转一定角度得到△ADN,
∴AN=BC,DN=CD=DB,△ADN是等腰直角三角形,
∵△BCD是等腰直角三角形,点Q是BC中点,
∴![]()
∵点P是AN中点,
∴![]()
∴![]()
∵∠NDP=∠CDQ=45°,
∴∠PDQ=∠PDN+∠CDN+∠CDQ=90°+∠CDN,
∵∠NDB=∠CDN+∠CDB=90°+∠CDN,
∴∠PDQ=∠NDB,
∵![]()
∴△PDQ∽△NDB,
∴![]()
∴![]()


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,大楼![]() (可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点
(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点![]() 和点
和点![]() 处,
处,![]() 、
、![]() 均在
均在![]() 的中垂线上,且
的中垂线上,且![]() 、
、![]() 到大楼的距离分别为
到大楼的距离分别为![]() 米和
米和![]() 米,又已知
米,又已知![]() 长
长![]() 米,
米,![]() 长
长![]() 米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.
米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和直线
和直线![]() .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x= 1 .
其中正确的有

A.1个 B.2个 C. 3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“欢乐跑中国重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了__分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中,小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.下图![]() 中的正方形网格中
中的正方形网格中![]() 是格点三角形,小正方形网格的边长为
是格点三角形,小正方形网格的边长为![]() (单位长度).
(单位长度).
![]() 的面积是________(平方单位);
的面积是________(平方单位);
![]() 在图
在图![]() 所示的正方形网格中作出格点
所示的正方形网格中作出格点![]() 和
和![]() ″
″![]() ″
″![]() ″,使
″,使![]() ,
,![]() ″
″![]() ″
″![]() ″
″![]() ,且
,且![]() 、
、![]() 、
、![]() ″
″![]() ″中任意两条线段的长度都不相等;
″中任意两条线段的长度都不相等;
![]() 在所有与
在所有与![]() 相似的格点三角形中,是否存在面积为
相似的格点三角形中,是否存在面积为![]() (平方单位)的格点三角形?如果存在,请在图
(平方单位)的格点三角形?如果存在,请在图![]() 中作出,如果不存在,请说明理由.
中作出,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△AOB中,∠A=90°,∠AOB=60°,OB=![]() ,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
(1)求OC、BC的长;
(2)设△CPQ的面积为S,求S与t的函数关系式;
(3)当P在OC上Q在ON上运动时,如图(2),设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△DEF中,下列六个条件中:①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F,不能判断△ABC与△DEF全等的是( )
A.①②④B.①②③C.④⑥①D.②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
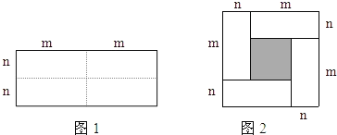
(1)请用两种不同的方法求图2中阴影部分的面积(直接用含m,n的代数式表示).
方法1:;
方法2:.
(2)根据(1)中的结论,请你写出代数式(m+n)2,(m-n)2,mn之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:已知实数a,b满足:a+b=5,ab=4,求a-b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com