
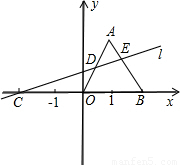
 ,
, ).
). ×2×
×2× =
=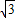 .
. ×4×y=2y,
×4×y=2y,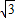 ,
, ,
,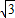 ),B(2,0)得直线AB解析式为y=-
),B(2,0)得直线AB解析式为y=-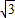 (x-2),
(x-2),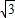 (x-2),
(x-2), ,
, ,
,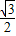 ),
),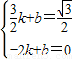 ,
,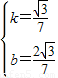 ,
,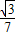 x+
x+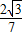 .
. x+
x+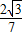 .
.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
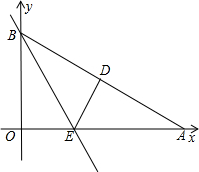 痕为BE.
痕为BE.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,A、B两点的坐标分别为(-3,0)、(0,3),C点在x轴的正半轴上,且到原点的距离为1.点P、Q分别从A、B两点同时出发,以相同的速度分别向x轴、y轴的正方向作匀速直线运动,直线PQ交直线AB于D.
如图,A、B两点的坐标分别为(-3,0)、(0,3),C点在x轴的正半轴上,且到原点的距离为1.点P、Q分别从A、B两点同时出发,以相同的速度分别向x轴、y轴的正方向作匀速直线运动,直线PQ交直线AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 180° |
| n |
| 180° |
| n |
查看答案和解析>>
科目:初中数学 来源:新课标读想练八年级数学(上) 题型:013
如图所示,正六边形ACDEFB,下列说法正确的个数为
[ ]
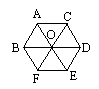
(1)可以看做是正△AOB绕O点连续旋转5次,旋转角为![]() 所形成的图形
所形成的图形
(2)可看做是菱形ABOC绕O点连续旋转2次,旋转角为![]() 所形成的图形
所形成的图形
(3)可以看做是四边形ABFC和四边形DEFC组成,且四边形DEFC是由四边形ABFC以CF为所在的直线为对称轴向右翻折![]() 得到的图形
得到的图形
(4)正六边形ACDEFB的对称轴有三条,分别是AE、BD、CF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com