
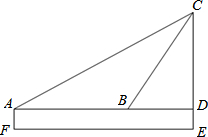
 九年级五班某同学为了测量某市电视台的高度,进行了如下操作:
九年级五班某同学为了测量某市电视台的高度,进行了如下操作:分析 由∠CAB=30°,∠CBD=60°,得到△ABC为等腰△,BC=AB=80,在Rt△CBD中,CD=$\frac{\sqrt{3}}{2}$BC=40$\sqrt{3}$,根据GE-EF=GF=12,计算出AE,然后由CE=CD+ED,得到CE.
解答 解:∵∠CAB=30°,∠CBD=60°,
∴∠ACB=30°,
∴∠CAB=∠ACB,
∴BC=AB=80,
在Rt△CBD中,CD=sin∠CBD•BC=$\frac{\sqrt{3}}{2}$×80=40$\sqrt{3}$,
CE=40$\sqrt{3}$+1.5≈70.7(米),
答:电视塔高度CE约为70.7米.
点评 本题考查了仰角的应用;也考查了把实际问题转化为数学问题的能力以及含30度的直角三角形三边的关系.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
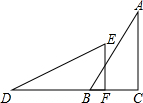 如图,△ABC≌△DEF,∠C=∠DFE=90°,A与D是 对应点,要使△DEF通过几何变换与△ABC重合,必须有的变换是( )
如图,△ABC≌△DEF,∠C=∠DFE=90°,A与D是 对应点,要使△DEF通过几何变换与△ABC重合,必须有的变换是( )| A. | 轴对称 | B. | 平移 | C. | 旋转 | D. | 中心对称 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
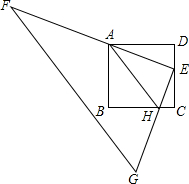 如图,正方形ABCD的边长为4,Rt△FEG的直角顶点E在正方形的边DC上运动,一条直角边EF始终经过点A,另一直角边EG交正方形的边BC于点H;
如图,正方形ABCD的边长为4,Rt△FEG的直角顶点E在正方形的边DC上运动,一条直角边EF始终经过点A,另一直角边EG交正方形的边BC于点H;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(1,-2),你能帮她求出其他各景点的坐标吗?
王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(1,-2),你能帮她求出其他各景点的坐标吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com