
【题目】(1)(探究)若![]() ,则代数式
,则代数式![]()
(类比)若![]() ,则
,则![]() 的值为 ;
的值为 ;
(2)(应用)当![]() 时,代数式
时,代数式![]() 的值是5,求当
的值是5,求当![]() 时,
时, ![]() 的值;
的值;
(3)(推广)当![]() 时,代数式
时,代数式![]() 的值为
的值为![]() ,当
,当![]() 时,
时,![]() 的值为 (含
的值为 (含![]() 的式子表)
的式子表)
【答案】(1)a2+2a;1;6;3;(2)3(3)m10
【解析】
(1)把代数式2a2+4a+4=2(a2+2a)+4,然后利用整体代入的方法计算;利用同样方法计算x23x5的值;
(2)先用已知条件得到p+q=4,而当x=1时,px3+qx+1=pq+1=(p+q)+1,然后利用整体代入的方法计算;
(3)利用当x=2020时,代数式ax5+bx3+cx5的值为m得到20205a+20203b+2020c=m+5,而当x=2020时,ax5+bx3+cx5=20205a20203b2020c5,然后利用整体代入的方法计算.
(1)∵a2+2a=1,
∴2a2+4a+4=2(a2+2a)+4=2×(1)+4=6;
若x23x=2,则x23x5=25=3;
故答案为a2+2a;1;6;3;
(2)∵当x=1时,代数式px3+qx+1的值是5,
∴p+q+1=5,
∴p+q=4,
∴当x=1时,px3+qx+1=pq+1=(p+q)+1=4+1=3;
(3)∵当x=2020时,代数式ax5+bx3+cx5的值为m,
∴20205a+20203b+2020c5=m,
即20205a+20203b+2020c=m+5,
当x=2020时,ax5+bx3+cx5=(2020)5a+(2020)3b+(2020)c5
=20205a20203b2020c5
=(20205a+20203b+2020c)5
=(m+5)5
=m55
=m10.
故答案为m10.


科目:初中数学 来源: 题型:
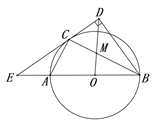
【题目】如图,Rt△ABC中,∠C=90°,⊙O是Rt△ABC的外接圆,过点C作⊙O的切线交BA的延长线于点E,BD⊥CE于点D,连接DO交BC于点M.
(1)求证:BC平分∠DBA;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
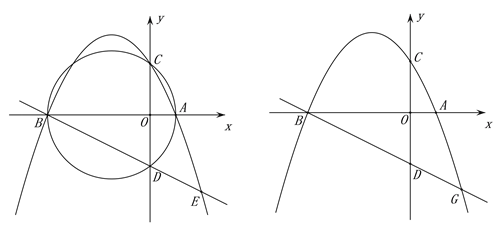
【题目】如图,已知抛物线y=-![]() x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.
x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.
(1)求此抛物线的表达式及圆心M的坐标;
(2)设P为弧BC上任意一点(不与点B,C重合),连接AP交y轴于点N,请问:AP·AN是否为定值,若是,请求出这个值;若不是,请说明理由;
(3)延长线段BD交抛物线于点E,设点F是线段BE上的任意一点(不含端点),连接AF.动点Q从点A出发,沿线段AF以每秒1个单位的速度运动到点F,再沿线段FB以每秒![]() 个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少?
个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书店老板去图书批发市场购买某种图书. 第一次用1200元购书若干本,并按该书定价7元出售,很快售完,由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了![]() ,他用1500元所购该书数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书. 试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
,他用1500元所购该书数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书. 试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其它因素)?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,…,第2018次输出的结果为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
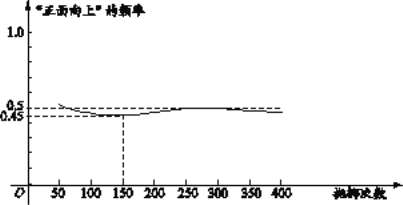
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小亮从点![]() 处出发,前进5米后向右转
处出发,前进5米后向右转![]() ,再前进5米后又向右转
,再前进5米后又向右转![]() ,这样走
,这样走![]() 次后恰好回到出发点
次后恰好回到出发点![]() 处.
处.
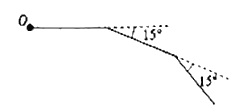
(1)小亮走出的这个![]() 边形的每个内角是多少度?这个
边形的每个内角是多少度?这个![]() 边形的内角和是多少度?
边形的内角和是多少度?
(2)小亮走出的这个![]() 边形的周长是多少米?
边形的周长是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,0°<∠BAC<90°,点A1,A3,A5…在边AB上,点 A2,A4,A6…在边AC上,且满足如下规律:A1A2⊥A2A3, A2A3⊥A3A4,A3A4⊥A4A5,…,若AA1=A1A2=A2A3=1,则A11A12的长度为()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过点A(0,4),B(-2,0),C(6,0).过点A作AD∥x轴交抛物线于点D,过点D作DE⊥x轴,垂足为E.M是四边形OADE的对角线的交点,点F在y轴的负半轴上,坐标为(0,-2).
(1)求抛物线所对应的函数表达式,并直接写出四边形OADE的形状;
(2)当点P,Q分别从C,F两点同时出发,均以每秒1个单位长度的速度沿CB,FA的方向运动,点P运动到点O时P,Q两点同时停止运动.设运动时间为t秒,在运动过程中,以P,Q,O,M四点为顶点的四边形的面积为S,求出S与t之间的函数表达式,并写出自变量的取值范围.
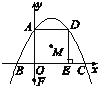
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com