
如图,抛物线y=x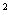 -2x+c的顶点A在直线l:y=x-5.
-2x+c的顶点A在直线l:y=x-5.
(1) 求抛物线顶点A的坐标;
(2) 设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3) 在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形,若存在,求点P的坐标;若不存在,请说明理由。
解:(1)∵顶点A的横坐标为x= =1,且顶点A在y=x﹣5上,
=1,且顶点A在y=x﹣5上,
∴当x=1时,y=1﹣5=﹣4,
∴A(1,﹣4).
(2) △ABD是直角三角形.
△ABD是直角三角形.
将A(1,﹣4)代入y =x2﹣2x+c,可得,1﹣2+c=﹣4,∴c=﹣3,
=x2﹣2x+c,可得,1﹣2+c=﹣4,∴c=﹣3,
∴y=x2﹣2x﹣3,∴B(0,﹣3)
当y=0时,x2﹣2x﹣3=0,x1=﹣1,x2=3
∴C(﹣1,0),D(3,0),
BD2=OB2+OD2=18,AB2=(4﹣3)2+12=2,AD2=(3﹣1)2 +42=20,
+42=20,
BD2+AB2=AD2,
∴∠ABD=90°,即△ABD是直角三角形.
(3)存在.
由题意知:直线y=x﹣5交y轴于点A(0,﹣5),交x轴于点F(5,0)
∴OE=OF=5,又∵OB=OD=3
∴△OEF与△OB D都是等腰直角三角形
D都是等腰直角三角形
∴BD∥l,即PA∥BD
则构成平行四边形只能是PADB或PABD,如图,
过点P作y轴的垂线,过点A作x轴的垂线并交于点C
设P(x1,x1﹣5),则G(1,x1﹣5)
则PC=|1﹣x1|,AG=|5﹣x1﹣4|=|1﹣x1|
PA=BD=3
由勾股定理得:
(1﹣x1)2+(1﹣x1)2=18,x12﹣2x1﹣8=0,x1=﹣2,4
∴P(﹣2,﹣7),P(4,﹣1)
存在点P(﹣2,﹣7)或P(4,﹣1)使以点A.B.D.P为顶点的四边形是平行四边形.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
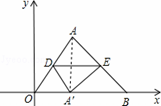
如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(3,4),点B的坐标为(6,0),D,E分别是线段AO,AB上的点,以DE所在直线为对称轴,把△ADE作轴对称变换得△A′DE,点A′恰好在x轴上若△OA′D与△OAB相似,则OA′的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
△ABC在平面直角坐标系xOy中的位置如图所示,点A的坐标为(-2,3),
点B的坐标为(-1,1),点C的坐标为(0,2).
(1)作△ABC关于点C成中心对称的△A1BlCl.
(2)将△A1BlCl向右平移4个单位,作出平移后的△A2B2C2.
 (3)点P是x轴上的一点,并且使得PA1+PC2的值最小,则点P的坐标为( , ).
(3)点P是x轴上的一点,并且使得PA1+PC2的值最小,则点P的坐标为( , ).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点E,F在函数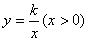 的图象上,直线EF分别与
的图象上,直线EF分别与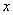 轴、
轴、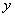 轴交于点A,B,且BE:BF=1:
轴交于点A,B,且BE:BF=1: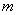 。过点E作EP⊥
。过点E作EP⊥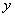 轴于P,,已知△OEP的面积为1,则
轴于P,,已知△OEP的面积为1,则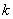 值是
值是  ,△OEF的面积是 (用含
,△OEF的面积是 (用含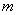 的式子表示)
的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com