
【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.
![]()
【答案】(1)点P 所表示的有理数是﹣3;(2)4(3)当点P表示的有理数与原点的距离是3个单位长度时,t值的值为1秒或3秒或5秒或7秒
【解析】
(1)根据P点的速度,有理数的加法,可得答案;
(2)根据两点间的距离公式,可得AB的长度,根据路程除以速度,可得时间;
(3)根据分类讨论:0≤t≤4,4≤t≤8,速度乘以时间等于路程,可得答案;
(4)根据绝对值的意义,可得P点表示的数,根据速度与时间的关系,可得答案.
(1)﹣6+3×1=﹣3,当t=1时,点P所表示的有理数是﹣3;
(2)当点P与点B重合时,点P所运动的路程为|6﹣(﹣6)|=12,
由路程除以速度得:t=12÷3=4;
(3)点P沿数轴由点A到点B再回到点A的运动过程中,点P与点A的距离分为两种情况:
当点P到达点B前,即0≤t≤4时,点P与点A的距离是3t;
当点P到达点B再回到点A的运动过程中,即4≤t≤8时,点P与点A的距离是:12-3(t-4)=24﹣3t;
(4)当点P表示的有理数与原点(设原点为O)的距离是3个单位长度时,P点表示的数是-3或3,则有以下四种情况:
当点P由点A到点O时:OP=AO﹣3t,即:6﹣3t=3,t=1;
当点P由点O到点B时:OP=3t﹣AO,即:3t﹣6=3,t=3;
当点P由点B到点O时:OP=18﹣3t,即:18﹣3t=3,t=5;
当点P由点O到A时:OP=3t﹣18,即:3t﹣18=3,t=7,
即:当点P表示的有理数与原点的距离是3个单位长度时,t值的值为1秒或3秒或5秒或7秒.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点![]() .
.
![]() 蜗牛离开出发点
蜗牛离开出发点![]() 最远时是多少厘米?
最远时是多少厘米?
![]() 在爬行过程中,如果每爬
在爬行过程中,如果每爬![]() 厘米奖励
厘米奖励![]() 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队同时修筑水渠,且两队所修水渠总长度相等.如图是两队所修水渠长度y(米)与修筑时间x(时)的函数图象的一部分.请根据图中信息,解答下列问题: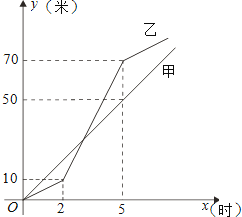
(1)①直接写出甲队在0≤x≤5的时间段内,y与x之间的函数关系式;
②直接写出乙队在2≤x≤5的时间段内,y与x之间的函数关系式;
(2)求开修几小时后,乙队修筑的水渠长度开始超过甲队?
(3)如果甲队施工速度不变,乙队在修筑5小时后,施工速度因故减少到5米/时,结果两队同时完成任务,求乙队从开修到完工所修水渠的长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
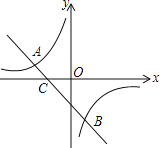
【题目】如图,已知A(﹣3,1),B(1, ![]() )是一次函数
)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出使一次函数的函数值小于反比例函数的函数值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
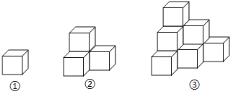
【题目】根据三视图求几何体的表面积.
下列各图是棱长为![]() 的小正方体摆成的,如图①中,共有
的小正方体摆成的,如图①中,共有![]() 个小正方体,从正面看有
个小正方体,从正面看有![]() 个正方形,表面积为
个正方形,表面积为![]() ;如图②中,共有
;如图②中,共有![]() 个小正方体,从正面看有
个小正方体,从正面看有![]() 个正方形,表面积为
个正方形,表面积为![]() ;如图③,共有
;如图③,共有![]() 个小正方体,从正面看有
个小正方体,从正面看有![]() 个正方形,表面积为
个正方形,表面积为![]() ;…
;…
![]() 第
第![]() 个图中,共有多少个小正方体?从正面看有多少个正方形?表面积是多少?
个图中,共有多少个小正方体?从正面看有多少个正方形?表面积是多少?
![]() 第
第![]() 个图形中,从正面看有多少个正方形?表面积是多少?
个图形中,从正面看有多少个正方形?表面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点E在AD上,点F在DC上,且∠BEF=∠A.
(1)∠BEF=(用含α的代数式表示);
(2)当AB=AD时,猜想线段EB、EF的数量关系,并证明你的猜想;
(3)当AB≠AD时,将“点E在AD上”改为“点E在AD的延长线上,且AE>AB,AB=mDE,AD=nDE”,其他条件不变(如图),求 ![]() 的值(用含m,n的代数式表示)
的值(用含m,n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,且
,且![]() .
.
![]()
![]() 则
则![]() ________,
________,![]() ________;并将这两个数在数轴上所对应的点
________;并将这两个数在数轴上所对应的点![]() ,
,![]() 表示出来;
表示出来;
![]() 数轴上在
数轴上在![]() 点右边有一点
点右边有一点![]() 到
到![]() 、
、![]() 两点的距离和为
两点的距离和为![]() ,若点
,若点![]() 的数轴上所对应的数为
的数轴上所对应的数为![]() ,求
,求![]() 的值;
的值;
![]() 若点
若点![]() ,点
,点![]() 同时沿数轴向正方向运动,点
同时沿数轴向正方向运动,点![]() 运动的速度为
运动的速度为![]() 单位/秒,点
单位/秒,点![]() 运动的速度为
运动的速度为![]() 单位/秒,若
单位/秒,若![]() ,求运动时间
,求运动时间![]() 的值.
的值.
(温馨提示:![]() 、
、![]() 之间距离记作
之间距离记作![]() ,点
,点![]() 、
、![]() 在数轴上对应的数分别为
在数轴上对应的数分别为![]() 、
、![]() ,则
,则![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:
表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:
(1)求![]() =________.
=________.
(2)若![]() =5,则x=____.
=5,则x=____.
(3)同理![]() 表示数轴上有理数x所对应的点到-1和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得
表示数轴上有理数x所对应的点到-1和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得![]() =3,这样的整数是________(直接写答案)
=3,这样的整数是________(直接写答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com