
【题目】已知关于x的一元二次方程![]() -(k+2)x+2k=0.
-(k+2)x+2k=0.
(1)试说明无论k取何值时,这个方程一定有实数根;
(2)已知等腰![]() 的一边a=1,若另两边b、c恰好是这个方程的两个根,求
的一边a=1,若另两边b、c恰好是这个方程的两个根,求![]() 的周长.
的周长.
【答案】(1)证明详见解析;(2)5.
【解析】
试题用一元二次方程的判别式来判断方程的解的情况,如果判别式大于0,说明一元二次方程有两个不相等的实数根,如果判别式等于0,说明一元二次方程有两个相等的实数根,如果判别式小于0,说明一元二次方程没有实数根.说明此方程有实数根,只要能证明该方程中得△≥0即可求解.
两腰b、c恰好是这个方程的两个根,说明此方程有两个相等的实数根.即△=0.由(1)可知k的取值,然后将k的值代入原方程求根.最后计算△ABC的周长即可.
试题解析:
解:(1)∵![]()
![]()
∴无论取何值时,方程一定有实数根.
由(1)可知:![]() ,即
,即![]()
解得:K=2
当![]() 时,
时,![]()
解得:![]()
即b=c=2
∴△ABC的周长=2+2+1=5


科目:初中数学 来源: 题型:
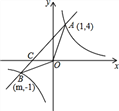
【题目】已知,如图,反比例函数y=![]() 的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
的图象与一次函数y=x+b的图象交于点A(1,4),点B(m,-1),
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出不等式x+b>![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善城市排水系统,某市需要新铺设一段全长为![]() 的排水管道.为了减少施工对城市交通的影响,实际施工时每天的工效是原计划的
的排水管道.为了减少施工对城市交通的影响,实际施工时每天的工效是原计划的![]() 倍,结果提前
倍,结果提前![]() 天完成这一任务.
天完成这一任务.
(1)这个工程队原计划每天铺设管道多少![]() ?
?
(2)在这项工程中,如果要求工程队提前![]() 天完成任务,那么实际施工时每天的工效比原计划增加的百分率是多少?
天完成任务,那么实际施工时每天的工效比原计划增加的百分率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形的纸片分别沿![]() 、
、![]() 折叠后,点
折叠后,点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,且
处,且![]() 、
、![]() 、
、![]() 三点刚好在同一直线上,折痕分别为
三点刚好在同一直线上,折痕分别为![]() 、
、![]() ,射线
,射线![]() 为
为![]() 的角平分线,则下列说法中:①
的角平分线,则下列说法中:①![]() 是
是![]() 的平分线;②
的平分线;②![]() 是
是![]() 的平分线;③
的平分线;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
(1)元旦期间,“茂业“商场对某品牌羽绒服实行七折销售,张阿姨到该商场购买了一件该品牌的羽绒服发现比不打折时可省下240元,那么该品牌的标价是多少元?
(2)某公司共有工人40人,已知一个工人每小时可制造10个![]() 种零件或20个
种零件或20个![]() 种零件,每个工人能而且只能制造其中的一种零件.
种零件,每个工人能而且只能制造其中的一种零件.
①如果这些工人每小时能制造![]() 、
、![]() 两种零件共550个,请问其中参加制造
两种零件共550个,请问其中参加制造![]() 种零件的工人有多少人?
种零件的工人有多少人?
②如果1个![]() 种零件与3个
种零件与3个![]() 种零件组合后能形成一个整件,为使这些工人每小时制造出的零件都能恰好组合成整件,那么应安排多少工人制造
种零件组合后能形成一个整件,为使这些工人每小时制造出的零件都能恰好组合成整件,那么应安排多少工人制造![]() 种零件?
种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
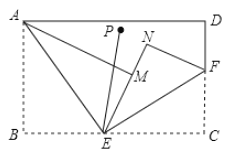
【题目】若等腰三角形的顶角为36°,则这个三角形就是黄金三角形。如图,在△ABC中,BA=BC,D 在边 CB 上,且 DB=DA=AC。

(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若 M为线段 BC上的点,过 M作直线MH⊥AD于 H,分别交直线 AB,AC与点N,E,如图 2,试写出线段 BN、CE、CD之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() 两种产品共10件,其生产成本和销售价如下表所示:
两种产品共10件,其生产成本和销售价如下表所示:
产品 |
|
|
成本(万元/件) | 3 | 5 |
售价(万元/件) | 4 | 7 |
(1)若工厂计划获利14万元,则应分别生产![]() 两种产品多少件?
两种产品多少件?
(2)若工厂投入资金不多于44万元,且获利不少于14万元,则工厂有哪些生产方案?
(3)在第(2)的条件下,哪种方案获利最大;最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com