Question

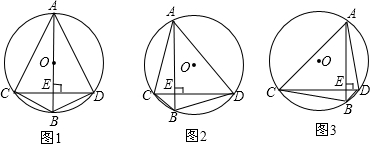
如图，线段CD是⊙O的弦，⊙O的半径是R，点A是优弧CD上的一个动点，作AB⊥CD于E（点E在线段CD上但不与点C﹑D重合），AB交⊙O于B，连接AC﹑CB﹑BD﹑DA．
（1）如图1，若AB经过圆心O，试探索AD﹑BC和R之间存在着什么样的数量关系？请用一个等式表达出来并证明你的结论．
（2）如图2﹑图3，若AB不经过圆心O时，你探索的上述结论是否依然成立？若不成立，请说明理由；若成立，请任意选一图证明．
（3）作OF⊥AD于F，试利用图1探索OF与BC之间存在着什么样的数量关系？请用一个等式表达出来（不要求证明）；你探索的这个结论在图2﹑图3中依然成立吗？（只要求回答成立还是不成立，不要求写理由或证明）．

Answer 1

分析：（1）根据垂径定理得出AC=AD，再利用圆周角定理求出∠ACB=90°，利用勾股定理求出即可；
（2）连接AO并延长到圆上一点M，连接DM，利用圆周角定理得出∠CAB=∠DAM，进而得出BC=DM，即可得出答案；
（3）首先得出FO=

1

2

DM，再利用垂径定理以及三角形中位线的性质即可得出．

解答：解：（1）（2R）²=AD²+BC²；
证明：∵AB⊥CD，AB交⊙O于B，
∴AC=AD，∠ACB=90°，
∴AB²=AC²+BC²，
即：（2R）²=AD²+BC²；

（2）连接AO并延长到圆上一点M，连接DM，
∵AM是圆O直径，
∴∠ADM=90°，
∵∠ACD=∠AMD，∠AEC=90°，
∴∠CAB=∠DAM，
∴BC=DM，
∵在Rt△ADM中，AD²+DM²=AM²，
DM=BC，AM=2R，
∴（2R）²=AD²+BC²；

（3）利用垂径定理以及三角形中位线的性质即可得出，OF=

1

2

BC，
这个结论在图2﹑图3中依然成立．

点评：此题主要考查了垂径定理以及圆周角定的综合应用、勾股定理的应用等知识，正确作出过圆心的直径构造出相等的圆周角，利用等量代换得出是解决问题的关键．