
����Ŀ������ͬѧ����һ����ϣ����������������г���M�س�����һ����·����ǰ��N�أ�������ʻ��ʱ��Ϊt��h������������֮��ľ���Ϊy��km����y��t�ĺ�����ϵ��ͼ1��ʾ��
����˼����������ͼ1�IJ�����ȷ��Ϣ�����ȳ���1h���׳���0.5Сʱ����������
�����������ͬѧ����������⣺

��1���ֱ�����߶�BC��CD����ֱ�ߵĺ�������ʽ��
��2����20��y��30ʱ����t��ȡֵ��Χ��
��3���ֱ�����ף�����ʻ��·��S����S����ʱ��t�ĺ�������ʽ������ͼ2������ֱ������ϵ�зֱ����ǵ�ͼ��
��4������Ħ�г�����ͬʱ��������N����ͬһ��·����ǰ��M�أ���������![]() h�����������ʱ����������ʱ�����������
h�����������ʱ����������ʱ�����������
���𰸡���1��ֱ��BC�Ľ���ʽΪ��y=40t��60��ֱ��CD�ĺ�������ʽΪ��y=��20t+80����2��![]() ��
��![]() ����3��S��=60t��60��
����3��S��=60t��60��![]() ����S��=20t��0��t��4����ͼ�����������4��������
����S��=20t��0��t��4����ͼ�����������4��������![]() h���������
h���������
��������
�����������1�����ô���ϵ������������ʽ�����ɽ��
��2��������ס��ҵ��ٶȡ�����OA�ĺ�������ʽΪ��y=20t��0��t��1�������Ե�A��������Ϊ20�����ݵ�20��y��30ʱ���õ�20��40t��60��30����20����20t+80��30���ⲻ��ʽ�鼴�ɣ�
��3���õ�S��=60t��60��![]() ����S��=20t��0��t��4������������ͼ�ɣ�
����S��=20t��0��t��4������������ͼ�ɣ�
��4��ȷ������M�ص�·��S����ʱ��t�ĺ�������ʽΪ��S��=��40t+80��0��t��2��������S��=��40t+80��S��=60t��60��ͼ��ĺ�����Ϊ![]() �����Ա�����
�����Ա�����![]() h���������
h���������
�⣺��1��ֱ��BC�ĺ�������ʽΪy=kt+b��
�ѣ�1.5��0������![]() ������ã�
������ã�
��ã�![]() ��
��
��ֱ��BC�Ľ���ʽΪ��y=40t��60��
��ֱ��CD�ĺ�������ʽΪy1=k1t+b1��
�ѣ�![]() ������4��0������ã�
������4��0������ã� ��
��
��ã� ��
��
��ֱ��CD�ĺ�������ʽΪ��y=��20t+80��
��2������ٶ�Ϊakm/h���ҵ��ٶ�Ϊbkm/h����������ã�
 ��
��
��ã�![]() ��
��
�����ٶ�Ϊ60km/h���ҵ��ٶ�Ϊ20km/h��
��OA�ĺ�������ʽΪ��y=20t��0��t��1�������Ե�A��������Ϊ20��
��20��y��30ʱ��
��20��40t��60��30����20����20t+80��30��
��ã�![]() ��
��![]() ��
��
��3����������ã�S��=60t��60��![]() ��
��
S��=20t��0��t��4����
����ͼ����ͼ2��ʾ��

��4����t=![]() ʱ��
ʱ��![]() ������M�ص�·��S����ʱ��t�ĺ�������ʽΪ��
������M�ص�·��S����ʱ��t�ĺ�������ʽΪ��
S��=��40t+80��0��t��2����
��ͼ3��

S��=��40t+80��S��=60t��60��ͼ��ĺ�����Ϊ![]() ��
��
���Ա�����![]() h���������
h���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪һ�κ���y����2x+1��ͼ��A��a��m����B��a+1��n�����㣬��m_____n���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����ݣ�9��8��8��6��9��5��7�����������ݵ���λ���ǣ�������
A. 6 B. 7 C. 8 D. 9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD��AB=AC��E��F�ֱ���BC��AD���е㣬����AE��CF��
��֤���ı���AECF�Ǿ��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,���ĸ�ͬ����С��ֱ��������,����ֱ�DZ߷ֱ�Ϊa,b,б��Ϊc,ƴ��һ��������,�м�����һ��С������.
��1����������֮��������ϵ,̽��������a,b,c�ĵ�ʽ.
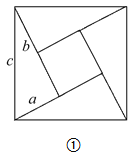
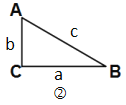
��2�����ã�1���з��ֵ�ֱ������������ֱ�DZ�a,b��б��c֮��Ĺ�ϵ���������:��ͼ����ֱ����ABC�У���C=90������c=6��a+b=8������ABC�����Ϊ__________
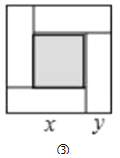
��3����ͼ�ۣ��������εı߳�Ϊm��С�����εı߳�Ϊn������x��y��ʾ�ĸ����ε����߳���x��y�����۲�ͼ����ָ�����¹�ϵʽ��
��1��![]() ��2��x+y=m ��3��x2��y2=mn
��2��x+y=m ��3��x2��y2=mn
��4��![]() ������ȷ����_________������ţ�
������ȷ����_________������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ��з��ź�ɫ����ɫ����ɫ����Ƥ����30�������dz���ɫ������ȫ��ͬ��С��ͨ���������������ִ���������ɫ����ɫ���Ƶ���ȶ���0.15��0.45֮�䣬��ڴ��к�ɫ��ĸ��������ǣ� ��
A. 14 B. 20 C. 9 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ�ֽ�����ȷ�ĸ���Ϊ( )
��x3��2xy��x=x(x2��2y)��
��x2��4x��4=(x��2)2��
����x2��y2=(x��y)(x��y)��
A��3�� B��2�� C��1�� D��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�����ABC �У�ADƽ�֡�BAC��AE��BC����B��40�㣬��C��70�㣮
(1)���DAE�Ķ�����
(2)��ͼ�ڣ����ѡ�AE��BC����ɡ���F��DA���ӳ����ϣ�FE��BC���������������䣬���DFE�Ķ�����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com