
【题目】如图,在矩形ABCD中,点E在边AD上,将此矩形沿CE折叠,点D落在点F处,连接BF,B、F、E三点恰好在一直线上.
(1)求证:△BEC为等腰三角形;(2)若AB=2,∠ABE=45°,求矩形ABCD的面积.

【答案】(1)证明见解析;(2)4![]() .
.
【解析】
试题(1)由矩形ABCD可得∠DEC=∠BCE,由折叠知∠DEC=∠FEC,从而可得 ∠FEC=∠BCE,从而可推得结论;
(2)利用勾股定理可求得BE的长,由(1)可知BC=BE,利用矩形的面积公式即可得.
试题解析:(1)∵四边形ABCD是矩形,∴AD∥BC,∴∠DEC=∠BCE,
由折叠知∠DEC=∠FEC,∴∠FEC=∠BCE,
又∵B、F、E三点在一直线上,∴∠BEC=∠BCE,
∴BC=BE,即△BEC为等腰三角形;
(2)∵四边形ABCD是矩形,∴∠A=90°,
又∵AB=2,∠ABE=45°,∴BE=2![]() ,
,
又∵BC=BE,∴BC=2![]() ,
,
∴矩形ABCD的面积为4![]() .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB的垂直平分线分别交AB,BC于D,E,AC的垂直平分线分别交AC,BC于F,G.
(1)若△AEG的周长为10,求线段BC的长.
(2)若∠BAC=128°,求∠EAG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骑共享单车已成为人们喜爱的一种绿色出行方式.已知A、B、C三家公司的共享单车都是按骑车时间收费,标准如下:
公司 | 单价(元/半小时) | 充值优惠 |
A | m | 充20元送5元,即:充20元实得25元 |
B | m-0.2 | 无 |
C | 1 | 充20元送20元,即:充20元实得40元 |
(注:使用这三家公司的共享单车,不足半小时均按半小时计费.用户的账户余额长期有效,但不可提现.)
4月初,李明注册成了A公司的用户,张红注册成了B公司的用户,并且两人在各自账户上分别充值20元.一个月下来,李明、张红两人使用单车的次数恰好相同,且每次都在半小时以内,结果到月底李明、张红的账户余额分别显示为5元、8元.
(1)求m的值;
(2)5月份,C公司在原标准的基础上又推出新优惠:每月的月初给用户送出5张免费使用券(1
次用车只能使用1张券).如果王磊每月使用单车的次数相同,且在30次以内,每次用车都不超过
半小时. 若要在这三家公司中选择一家并充值20元,仅从资费角度考虑,请你帮他作出选择,并说
明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A( ![]() ,1)关于x轴的对称点为点A1 , 将OA绕原点O逆时针方向旋转90°到OA2 , 用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为 .
,1)关于x轴的对称点为点A1 , 将OA绕原点O逆时针方向旋转90°到OA2 , 用扇形OA1A2围成一个圆锥,则该圆锥的底面圆的半径为 . 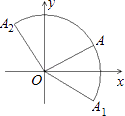
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将油箱注满k升油后,轿车行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S= ![]() (k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶760千米,当平均耗油量为0.08升/千米时,该轿车可以行驶千米.
(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶760千米,当平均耗油量为0.08升/千米时,该轿车可以行驶千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:

(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com