练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中：： =1：2：3则BC：AC：AB=（ ）

    A.1：2：3B.1：2：

    C.1：：2D.3：2：1

    【答案】C

    【解析】

    根据三角形内角和定理和这个三角形三个角的度数之比，可以分别求出这个三角形的三个角的度数分别是30°、60°、90°，所以这个三角形是直角三角形，根据30度所对的直角边等于斜边的一半，设30°所对的直角边BC=x，则斜边AB=2x，再根据勾股定理求出第三条边AC=x，据此即可求出它们的比．

    因为∠A:∠B:∠C=1:2:3

    1+2+3=6

    所以∠A=180°×=30°

    ∠B=180°×=60°

    ∠C=180°×=90°

    设直角边BC=x,则斜边AB=2x,根据勾股定理求出第三条边AC= =x，

    则BC:AC:AB=x:x:2x=1::2

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE=DF．

    （1）求证：ABCD是菱形；

    （2）若AB=5，AC=6，求ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于题目“一段抛物线L：y=﹣x（x﹣3）+c（0≤x≤3）与直线l：y=x+2有唯一公共点，若c为整数，确定所有c的值，”甲的结果是c=1，乙的结果是c=3或4，则（　　）

    A. 甲的结果正确

    B. 乙的结果正确

    C. 甲、乙的结果合在一起才正确

    D. 甲、乙的结果合在一起也不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠A＝20°，CD是∠BCA的平分线，△CDA中，DE是CA边上的高，又有∠EDA＝∠CDB，求∠B的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读下列解题过程，然后解答后面两个问题．

    解方程：|x-3|=2．

    解：当x-3≥0时，原方程可化为x-3=2，解得x=5；

    当x-3＜0时，原方程可化为x-3=-2，解得x=1．

    所以原方程的解是x=5或x=1．

    （1）解方程：|3x-2|-4=0．

    （2）解关于x的方程：|x-2|=b+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小英和小倩站在正方形的对角A，C两点处，小英以2米/秒的速度走向点D处，途中位置记为P，小倩以3米/秒的速度走向点B处，途中位置记为Q，假设两人同时出发，已知正方形的边长为8米，E在AB上，AE=6米，记三角形AEP的面积为S1平方米，三角形BEQ的面积为S2平方米，如图所示．

    （1）她们出发后几秒时S1=S2；

    （2）当S1+S2=15时，小倩距离点B处还有多远？

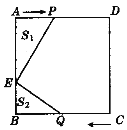
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论，其中,正确结论的个数是(　　)

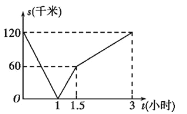
    ①出发1小时时,甲、乙在途中相遇;

    ②乙开车速度是80千米/小时；

    ③出发1.5小时时,乙比甲多行驶了60千米;

    ④出发3小时时,甲、乙同时到达终点;

    A. 1B. 2C. 3D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

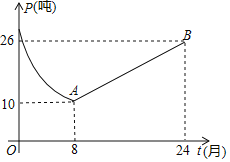
    【题目】某药厂销售部门根据市场调研结果，对该厂生产的一种新型原料药未来两年的销售进行预测，井建立如下模型：设第t个月该原料药的月销售量为P（单位：吨），P与t之间存在如图所示的函数关系，其图象是函数P=（0＜t≤8）的图象与线段AB的组合；设第t个月销售该原料药每吨的毛利润为Q（单位：万元），Q与t之间满足如下关系：Q=

    （1）当8＜t≤24时，求P关于t的函数解析式；

    （2）设第t个月销售该原料药的月毛利润为w（单位：万元）

    ①求w关于t的函数解析式；

    ②该药厂销售部门分析认为，336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围，求此范围所对应的月销售量P的最小值和最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题提出）

    学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

    （初步思考）

    我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

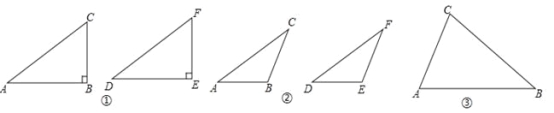
    （深入探究）

    第一种情况：当∠B是直角时，△ABC≌△DEF．

    （1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ，可以知道Rt△ABC≌Rt△DEF．

    第二种情况：当∠B是钝角时，△ABC≌△DEF．

    （2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．

    第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．

    （3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）

    （4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若 ，则△ABC≌△DEF．

    查看答案和解析>>

    同步练习册答案