
分析 根据二次根式有意义的条件得到a(x-a)≥0,x-a≥0,则a≥0,而a(y-a)≥0,a-y≥0,则a≤0,得到a=0,把a=0代入已知条件中易得x=-y,然后把x=-y代入分式计算即可.
解答 解:∵a(x-a)≥0,x-a≥0,
∴a≥0,
又∵a(y-a)≥0,a-y≥0,
∴a≤0,
∴a=0,
把a=0代入已知条件则$\sqrt{x}$-$\sqrt{-y}$=0,
∴x=-y,
∴原式=$\frac{3{y}^{2}-{y}^{2}-{y}^{2}}{{y}^{2}-{y}^{2}+{y}^{2}}$=1,
故答案为:1.
点评 本题考查了分式的化简求值:先根据二次根式有意义的条件得到字母的值或关系,然后代入所求的分式中进行计算.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩 | 81 | 85 | 88 | 91 |
| 人数 | 1 | 4 | 2 | 3 |
| A. | 91,87 | B. | 85,87 | C. | 88,86 | D. | 83,88 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
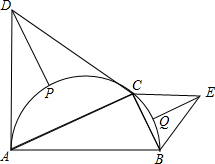 如图,C是以AB为直径的半圆O上一点.连结AC,BC,分别以AC,BC为边A外作正△ACD,正△BEC,P,Q分别是弧$\widehat{AC}$,弧$\widehat{BC}$的中点,若DP+EQ=11,AB=13,则AC+BC的长是( )
如图,C是以AB为直径的半圆O上一点.连结AC,BC,分别以AC,BC为边A外作正△ACD,正△BEC,P,Q分别是弧$\widehat{AC}$,弧$\widehat{BC}$的中点,若DP+EQ=11,AB=13,则AC+BC的长是( )| A. | 24 | B. | 12$\sqrt{3}$+12 | C. | 24$\sqrt{3}$-24 | D. | 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1或2 | B. | 0或2 | C. | 2 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com