
 如图,四边形ABCD为⊙O的内接四边形,连接AC、BO,已知∠CAB=36°,∠ABO=30°,则∠D=96°.
如图,四边形ABCD为⊙O的内接四边形,连接AC、BO,已知∠CAB=36°,∠ABO=30°,则∠D=96°. 分析 连结OC,如图,根据圆周角定理得到∠BOC=2∠CAB=72°,再根据等腰三角形的性质和三角形内角和定理可计算出∠OBC=54°,则∠ABC=∠OBA+∠OBC=84°,然后根据圆内接四边形的性质求∠D的度数.
解答 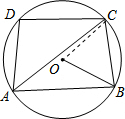 解:连结OC,如图,
解:连结OC,如图,
∠BOC=2∠CAB=2×36°=72°,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠OBC=$\frac{1}{2}$(180°-∠BOC)=$\frac{1}{2}$(180°-72°)=54°,
∴∠ABC=∠OBA+∠OBC=30°+54°=84°,
∵∠D+∠ABC=180°,
∴∠D=180°-84°=96°.
故答案为96.
点评 本题考查了圆内接四边形的性质:圆内接四边形的对角互补;任意一个外角等于它的内对角.也考查了圆周角定理.


科目:初中数学 来源: 题型:解答题
 如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成50°角,在离电线杆底部D点6米的B处安置测角仪,测角仪高AB为1.5米,在A处测得电线杆上C处的仰角为32°,求拉线CE的长(结果精确到0.1米).(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.63,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成50°角,在离电线杆底部D点6米的B处安置测角仪,测角仪高AB为1.5米,在A处测得电线杆上C处的仰角为32°,求拉线CE的长(结果精确到0.1米).(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.63,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 13 | D. | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com