练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
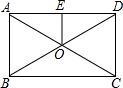
    1．如图，已知：矩形ABCD中对角线，AC，BD交于点O，E是AD中点，连接OE．若OE=3，AD=8，则对角线AC的长为（　　）
    A．5B．6C．8D．10

    分析 由矩形的性质得出OA=OC，∠ADC=90°，证出OE是△ACD的中位线，由三角形中位线定理得出CD=2OE=6，再由勾股定理求出AC即可．

    解答 解：∵四边形ABCD是矩形，
    ∴OA=OC，∠ADC=90°，
    ∵E是AD中点，
    ∴OE是△ACD的中位线，
    ∴CD=2OE=6，
    ∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10；
    故选：D．

    点评 此题考查了平行四边形的性质、三角形中位线定理、勾股定理；熟练掌握平行四边形的性质，由三角形中位线定理求出CD是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．在某次试验数据整理过程中，某个事件发生的频率情况如下表所示．
    试验次数105010020050010002000
    事件发生的频率0.2450.2480.2510.2530.2490.2520.251
    估计这个事件发生的概率是0.25（精确到0.01），试举出一个随机事件的例子，使它发生的概率与上述事件发生的概率大致相同：从红桃A、黑桃A、梅花A、方块A四张牌中，随机抽取一张，则抽到方块A的概率为0.25．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

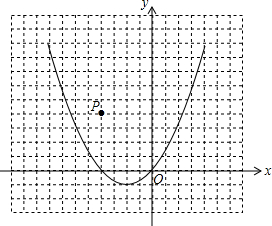    12．已知二次函数y=x2+x的图象，如图所示
    （1）根据方程的根与函数图象之间的关系，将方程x2+x=1的根在图上近似地表示出来（描点），并观察图象，写出方程x2+x=1的根（精确到0.1）．
    （2）在同一直角坐标系中画出一次函数y=$\frac{1}{2}$x+$\frac{3}{2}$的图象，观察图象写出自变量x取值在什么范围时，一次函数的值小于二次函数的值．
    （3）如图，点P是坐标平面上的一点，并在网格的格点上，请选择一种适当的平移方法，使平移后二次函数图象的顶点落在P点上，写出平移后二次函数图象的函数表达式，并判断点P是否在函数y=$\frac{1}{2}$x+$\frac{3}{2}$的图象上，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．已知二次函数y=ax2-bx-2（a≠0）的图象的顶点在第四象限，且过点（-1，0），当a-b为整数时，ab的值为（　　）
    A．$\frac{3}{4}$或1B．$\frac{1}{4}$或1C．$\frac{3}{4}$或$\frac{1}{2}$D．$\frac{1}{4}$或$\frac{3}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2，再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3，以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是（21008，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如图，在网格中（每个小正方形的边长均为1个单位）选取9个格点（格线的交点称为格点）．如果以A为圆心，r为半径画圆，选取的格点中除点A外恰好有3个在圆内，则r的取值范围为（　　）
    A．2$\sqrt{2}$＜r≤$\sqrt{17}$B．$\sqrt{17}$＜r≤3$\sqrt{2}$C．$\sqrt{17}$＜r≤5D．5＜r≤$\sqrt{29}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，在△ABC和△BCD中，∠BAC=∠BCD=90°，AB=AC，CB=CD．延长CA至点E，使AE=AC；延长CB至点F，使BF=BC．连接AD，AF，DF，EF．延长DB交EF于点N．

    （1）求证：AD=AF；
    （2）求证：BD=EF；
    （3）试判断四边形ABNE的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．某社区青年志愿者小分队年龄情况如下表所示：
    年龄（岁）1819202122
    人数25221
    则这12名队员年龄的众数、中位数分别是（　　）
    A．2，20岁B．2，19岁C．19岁，20岁D．19岁，19岁

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知：如图，在菱形ABCD中，点E、F分别为边CD、AD的中点，连接AE，CF，求证：△ADE≌△CDF．

    查看答案和解析>>

    同步练习册答案