
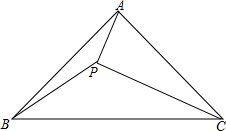
 如图,等腰Rt△ABC中,∠BAC=90°,点P为△ABC内一点,若AP=3,BP=5,CP=7,求△ABC的面积.
如图,等腰Rt△ABC中,∠BAC=90°,点P为△ABC内一点,若AP=3,BP=5,CP=7,求△ABC的面积. 分析 作辅助线,构建点P关于BC、AB、AC的对称点R、O、Q,把△ABC扩大为原来的2倍,组成五边形OBRCQ,求这个五边形OBRCQ的面积,可以得到结论;注意说明O、A、Q三点共线.
解答 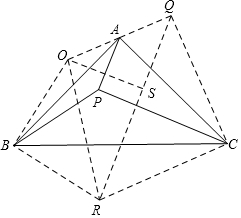 解:作P关于BC、AB、AC的对称点R、O、Q,
解:作P关于BC、AB、AC的对称点R、O、Q,
连接OA、AQ、CQ、CR、BR、OB、OR、QR,
过O作OS⊥QR于S,
∵BO=BP=BR=3,
AP=AQ=AO=5,
PC=CQ=CR=7,
∠OAB=∠PAB,∠PAC=∠CAQ,
∵∠PAB+∠PAC=∠BAC=90°,
∴∠OAB+CAQ=90°,
∴∠OAB+∠BAC+CAQ=180°,
∴O、A、Q三点共线,
同理∠OBR=∠RCQ=90°,
∴S△OBR=$\frac{1}{2}$×5×5=$\frac{25}{2}$,
S△QRC=$\frac{1}{2}$×7×7=$\frac{49}{2}$,
∵OB=BR,∠OBR=90°,
∴△OBR是等腰直角三角形,
∴OR=$\sqrt{2}$OB=5$\sqrt{2}$,
同理RQ=7$\sqrt{2}$,
设RS=x,
在Rt△ORS中,OR2-RS2=OS2,
在Rt△OSQ中,OQ2-QS2=OS2,
∴OR2-RS2=OQ2-QS2,
∴(5$\sqrt{2}$)2-x2=62-(7$\sqrt{2}$-x)2,
解得:x=4$\sqrt{2}$,
∴OS=$\sqrt{(5\sqrt{2})^{2}-(4\sqrt{2})^{2}}$=3$\sqrt{2}$,
∴S△ORQ=$\frac{1}{2}$RQ•OS=$\frac{1}{2}$×7$\sqrt{2}$×3$\sqrt{2}$=21,
∴S五边形OBRSQ=21+$\frac{25}{2}$+$\frac{49}{2}$=58,
∴S△ABC=$\frac{1}{2}$×58=29.
点评 本题考查了等腰直角三角形的性质及轴对称的性质,难度较大,图形也比较复杂;构建五边形是本题的关键,将五边形分成三个三角形计算其面积,才使问题得以解决.


科目:初中数学 来源: 题型:填空题
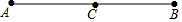 如图所示,线段AB长为a,点C是AB的中点,点D在AB上,若CD=b(b<$\frac{a}{2}$),则线段AD的长为$\frac{1}{2}$a-b或$\frac{1}{2}$a+b.
如图所示,线段AB长为a,点C是AB的中点,点D在AB上,若CD=b(b<$\frac{a}{2}$),则线段AD的长为$\frac{1}{2}$a-b或$\frac{1}{2}$a+b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
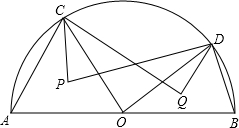 如图已知AB为半⊙O的直径,C、D为弧$\widehat{AB}$上两点,P、Q分别为△OAC、△OBD的外心.证明:CP•CQ=DP•DQ.
如图已知AB为半⊙O的直径,C、D为弧$\widehat{AB}$上两点,P、Q分别为△OAC、△OBD的外心.证明:CP•CQ=DP•DQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
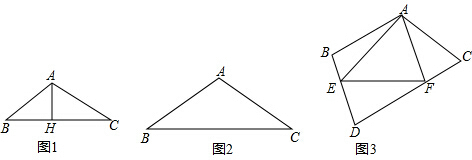
 如图,ABCD是正方形,E是边CD上(除端点外)任意一点,AM⊥BE于点M,CN⊥BE于点N,下列结论一定成立的有( )个.
如图,ABCD是正方形,E是边CD上(除端点外)任意一点,AM⊥BE于点M,CN⊥BE于点N,下列结论一定成立的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com