
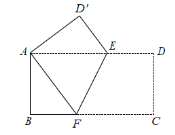
【题目】如图,把一张长方形纸片 ABCD 折叠起来,使其对角顶点 A,C 重合,若其长 BC 为 9,宽 AB 为 3.
⑴求证:△AEF 是等腰三角形;
⑵EF= .
【答案】(1)见详解;(2)![]()
【解析】
(1) 由折叠可知,∠EFC=∠AFE,根据AD∥BC,得到∠AEF=∠EFC,可得∠AEF=∠AFE,即可得出结论;
(2)过点F作FH⊥AD,设BF=x,则AF=CF=9x,求出x的值,再根据勾股定理即可得出EF=![]() =
=![]() .
.
(1)证明:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠AEF=∠EFC.
由折叠可知,∠EFC=∠AFE,
∴∠AEF=∠AFE.
∴AE=AF.
∴△AEF是等腰三角形.
(2)解:如图,过点F作FH⊥AD,
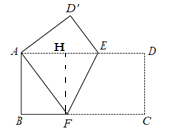
设BF=x,
则AF=CF=9x,
在Rt△ABF中,由BF2+AB2=AF2可得x2+32=(9x)2,
解得:x=4,
∴AF=FC=9-4=5,
∴AE=AF=5,
∵四边形ABFH是矩形,
∴AH=BF=4,AB=HF=3
∴HE=AE-AH=1,
∴EF=![]() =
=![]() =
=![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成.根据两队每天的工程费用和每天完成的工程量可知,若由两队合做此项维修工程,6天可以完成,共需工程费用385200元,若单独完成此项维修工程,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元,(1)若甲单独完成需要多少天?(2)从节省资金的角度考虑,应该选择哪个工程队?
查看答案和解析>>
科目:初中数学 来源: 题型:
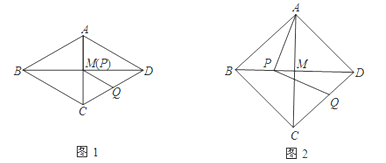
【题目】在△ABC中,BA=BC,∠BAC=α,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2α得到线段PQ.
(1)若α=60°,且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D,此时∠CDB的度数为________
(2)在图2中,点P不与点B、M重合,线段CQ的延长线交射线BM于点D,则∠CDB的度数为(用含α的代数式表示)________.
(3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B、M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=DQ,则α的取值范围是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如下:
频率分布统计表 | 频率分布直方图 | ||
分数段 | 频数 | 频率 |
|
60≤x<70 | 40 | 0.40 | |
70≤x<80 | 35 | b | |
80≤x<90 | a | 0.15 | |
90≤x<100 | 10 | 0.10 | |
请根据上述信息,解答下列问题:
(1)表中:a= ,b= ;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
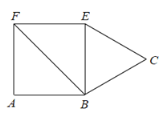
【题目】如图,正方形 ABEF 的面积为 4,△BCE 是等边三角形,点 C 在正方形ABEF 外,在对角线 BF 上有一点 P,使 PC+PE 最小,则这个最小值的平方为( )
A.![]() B.
B.![]() C.12D.
C.12D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F,则下列结论正确的是( )

A. 点F在BC边的垂直平分线上 B. 点F在∠BAC的平分线上
C. △BCF是等腰三角形 D. △BCF是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里吨),铁路运价为1元/(公里吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.
问:(1)这家食品厂到A地的距离是多少?
(2)这家食品厂此次买进的原料每吨5000元,卖出的食品每吨10000元,此批食品销售完后工厂共获利多少元?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一长方形鸡场,鸡场的一边靠墙(墙长 18 米),另三边用竹篱笆围成,竹篱笆的总长为 35 米,与墙平行的边留有 1 米宽的门(门用其它材料做成),若鸡场的面积为 160 平方米,则鸡场与墙垂直的边长为( )
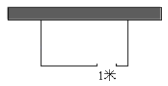
A.7.5 米B.8米C.10米D.10米或8米
查看答案和解析>>
科目:初中数学 来源: 题型:
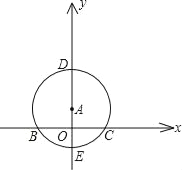
【题目】已知:如图,点A在y轴上,⊙A与x轴交于B、C两点,与y轴交于点D(0,3)和点E(0,﹣1)
(1)求经过B、E、C三点的二次函数的解析式;
(2)若经过第一、二、三象限的一动直线切⊙A于点P(s,t),与x轴交于点M,连接PA并延长与⊙A交于点Q,设Q点的纵坐标为y,求y关于t的函数关系式,并观察图形写出自变量t的取值范围;
(3)在(2)的条件下,当y=0时,求切线PM的解析式,并借助函数图象,求出(1)中抛物线在切线PM下方的点的横坐标x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com