提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度y(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0,当车流密度不超过25辆/千米时,车流速度为70千米/小时,研究表明:当25≤x≤200时,车流速度y是车流密度x的一次函数.
(1)当0≤x≤200时,求函数y与x的函数关系式;
(2)当车流密度x为多大时,车流量(单位时间通过桥上某观测点的车辆数,单位:辆/小时)w=x•y可以达到最大,并求出最大值.
解:(1)当0≤x≤25时,车流速度为y=70,
当25<x≤200时,设y与x的函数关系式为y=kx+b(k≠0,k、b为常数),
则图象经过点(25,70),(200,0),
所以,
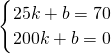
,
解得
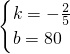
,
此时y=-

x+80,
所以,函数y与x的函数关系式为y=

;
(2)w=x•y=x(-

x+80)=-

x
2+80x=-

(x-200x+10000)
2+4000=-

(x-100)
2+4000,
即w=-

(x-100)
2+4000,
所以,当车流密度x=100时,车流量w有最大值,为4000辆/小时.
分析:(1)分0≤x≤25时,根据题意车流速度为定值70千米/小时,25<x≤200时,设y与x的函数关系式为y=kx+b(k≠0,k、b为常数),根据图象经过点(25,70),(200,0),利用待定系数法求一次函数解析式解答;
(2)把y换成关于x的关系式,整理并写成顶点式解析式,再根据抛物线的最值问题解答即可.
点评:本题考查的是二次函数在实际生活中的应用,主要利用了待定系数法求一次函数解析式,二次函数的最值问题,(1)要注意根据自变量的取值范围分段求解.

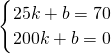 ,
,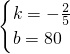 ,
, x+80,
x+80, ;
; x+80)=-
x+80)=- x2+80x=-
x2+80x=- (x-200x+10000)2+4000=-
(x-200x+10000)2+4000=- (x-100)2+4000,
(x-100)2+4000, (x-100)2+4000,
(x-100)2+4000,

